
分析 (1)由已知求得公差,再由等差数列前n项和求得答案;
(2)把k=-$\frac{1}{2}$代入an+1=k(an+an+2),可得an+2+an+1=-(an+1+an),an+3+an+2=-(an+2+an+1)=an+1+an,然后分n为奇数和偶数求得Sn;
(3)设数列{an}是等比数列,则它的公比q=$\frac{{a}_{2}}{{a}_{1}}$=a,得到${a}_{m}={a}^{m-1},{a}_{m+1}={a}^{m},{a}_{m+2}={a}^{m+1}$,然后分若am+1为等差中项,am为等差中项和am+2为等差中项三类求解得答案.
解答 解:(1)∵a1=1,a2=a,且an+1=k(an+an+2),
∴1+n(a-1)=k[1+(n-1)(a-1)+1+(n+1)(a-1)],解得k=$\frac{1}{2}$.
${S}_{n}=n+\frac{n(n-1)(a-1)}{2}$=$\frac{(a-1){n}^{2}-(a-3)n}{2}$;
(2)由a=1,k=-$\frac{1}{2}$,得${a}_{n+1}=-\frac{1}{2}({a}_{n}+{a}_{n+2})$,
∴an+2+an+1=-(an+1+an),an+3+an+2=-(an+2+an+1)=an+1+an,
当n是偶数时,Sn=a1+a2+a3+a4+…+an-1+an
=(a1+a2)+(a3+a4)+…+(an-1+an)
=$\frac{n}{2}$(a1+a2)=n.
当n是奇数时,Sn=a1+a2+a3+a4+…+an-1+an
=a1+(a2+a3)+(a4+a5)+…+(an-1+an)
=a1+$\frac{n-1}{2}$(a2+a3)=a1+$\frac{n-1}{2}$[-(a1+a2)]
=1-(n-1)=2-n,n=1也适合上式,
综上可得,Sn=$\left\{\begin{array}{l}{2-n,(n=2k-1,k∈{N}^{*})}\\{n,(n=2k,k∈{N}^{*})}\end{array}\right.$;
(3)设数列{an}是等比数列,则它的公比q=$\frac{{a}_{2}}{{a}_{1}}$=a,
∴${a}_{m}={a}^{m-1},{a}_{m+1}={a}^{m},{a}_{m+2}={a}^{m+1}$,
①若am+1为等差中项,则2am+1=am+am+2,
即2am=am-1+am+1,解得:a=1,不合题意;
②若am为等差中项,则2am=am+1+am+2,
即2am-1=am+am+1,化简得:a2+a-2=0,
解得a=-2(舍1);k=$\frac{{a}_{m+1}}{{a}_{m}+{a}_{m+2}}=\frac{{a}^{m}}{{a}^{m-1}+{a}^{m+1}}=\frac{a}{1+{a}^{2}}$=-$\frac{2}{5}$;
③若am+2为等差中项,则2am+2=am+1+am,
即2am+1=am+am-1,化简得:2a2-a-1=0,
解得a=-$\frac{1}{2}$;k=$\frac{{a}_{m+1}}{{a}_{m}+{a}_{m+2}}=\frac{{a}^{m}}{{a}^{m-1}+{a}^{m+1}}=\frac{a}{1+{a}^{2}}$=-$\frac{2}{5}$.
综上可得,满足要求的实数k有且仅有一个,k=-$\frac{2}{5}$.
点评 本题考查数列递推式,考查满足条件的实数值的求法,考查数列的前n项和公式的求法,解题时要注意等差数列和等比数列的性质的合理运用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
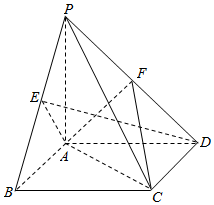 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com