
分析 (1)首先利用坐标表示($\overrightarrow{b}$+$\overrightarrow{c}$),然后根据向量平行求得sinx的值,根据角的范围求x;
(2)由数量积公式得到f(x)的表达式,根据正弦函数的有界性求最小值.
解答 解:(1)∵$\overrightarrow{b}$+$\overrightarrow{c}$=(sin x-1,-1),又$\overrightarrow{a}$∥($\overrightarrow{b}$+$\overrightarrow{c}$),
∴-(2+sin x)=sin x-1,即sin x=-$\frac{1}{2}$.
又x∈[-$\frac{π}{2}$,$\frac{π}{2}$],∴x=-$\frac{π}{6}$.
(2)∵$\overrightarrow{a}$=(2+sin x,1),$\overrightarrow{b}$=(2,-2),
∴f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=2(2+sin x)-2=2sin x+2.
又x∈R,
∴当sin x=-1时,f(x)有最小值,且最小值为0.
点评 本题考查了平面向量的加法、向量平行以及数量积的坐标运算;属于基础题.


科目:高中数学 来源: 题型:解答题
第3个月 第4个月 | 租用a型车 | 租用b型车 |
| 租用a型车 | 60% | 50% |
| 租用b型车 | 40% | 50% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
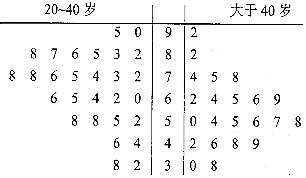 某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.| 购买意愿强 | 购买意愿弱 | 合计 | |
| 20-40岁 | |||
| 大于40岁 | |||
| 合计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 2 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com