
分析 (1)由数列的通项公式,当n=1,n=2,n=3时,分别求得a2,a3,a4的值;
(2)an+1-an=n+2(n∈N*),采用“累加法”即可求得{an}的通项公式.
解答 解:(1)由an+1-an=n+2(n∈N*),由an+1=an+n+2,a1=1,
a2=a1+1+2=4,
a3=a2+2+2=8,
a4=a3+3+2=13,
a2=4,a3=8,a4=13;
(2)an+1-an=n+2(n∈N*),
a2-a1=1+2,
a3-a2=2+2,
a4-a3=3+2,
…
an-an-1=n-1+2;
以上各式相加可得:an-a1=1+2+3+…+n-1+2(n-1),
∴an=1+$\frac{n(n-1)}{2}$+2(n-1),
=$\frac{{n}^{2}+3n-2}{2}$,
∴{an}的通项公式an=$\frac{{n}^{2}+3n-2}{2}$.
点评 本题考查数列的递推公式,考查“累加法”求数列的通项公式及等差数列通项公式,属于中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,e) | B. | [1,3] | C. | (3,+∞) | D. | (e,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
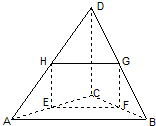 在空间四边形ABCD中,E,F,G,H分别是AC,BC,BD,DA的中点,若$AB=12\sqrt{2}$,$CD=4\sqrt{2}$,且四边形EFGH的面积为$12\sqrt{3}$,则AB和CD所成的角为60°.
在空间四边形ABCD中,E,F,G,H分别是AC,BC,BD,DA的中点,若$AB=12\sqrt{2}$,$CD=4\sqrt{2}$,且四边形EFGH的面积为$12\sqrt{3}$,则AB和CD所成的角为60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 左上方 | B. | 左下方 | C. | 右上方 | D. | 右下方 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com