
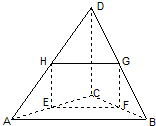
 在空间四边形ABCD中,E,F,G,H分别是AC,BC,BD,DA的中点,若$AB=12\sqrt{2}$,$CD=4\sqrt{2}$,且四边形EFGH的面积为$12\sqrt{3}$,则AB和CD所成的角为60°.
在空间四边形ABCD中,E,F,G,H分别是AC,BC,BD,DA的中点,若$AB=12\sqrt{2}$,$CD=4\sqrt{2}$,且四边形EFGH的面积为$12\sqrt{3}$,则AB和CD所成的角为60°. 分析 推导出四边形EFGH是平行四边形,设AB与CD所成角为θ,则sin∠HEF=sinθ,从而S平行四边形EFGH=HE•EF•sinθ=12$\sqrt{3}$,由此能求出AB和CD所成的角.
解答 解:∵在空间四边形ABCD中,E,F,G,H分别是AC,BC,BD,DA的中点,
$AB=12\sqrt{2}$,$CD=4\sqrt{2}$,
∴HG$\underset{∥}{=}$$\frac{1}{2}$AB,EF$\underset{∥}{=}$$\frac{1}{2}$AB,∴HG$\underset{∥}{=}$EF,且HG=EF=6$\sqrt{2}$,
HE$\underset{∥}{=}$$\frac{1}{2}$CD,GF$\underset{∥}{=}$$\frac{1}{2}$CD,∴HE$\underset{∥}{=}$GF,且HE=GF=2$\sqrt{2}$,
∴四边形EFGH是平行四边形,
设AB与CD所成角为θ,则sin∠HEF=sinθ,
∵四边形EFGH的面积为$12\sqrt{3}$,
∴S平行四边形EFGH=HE•EF•sinθ=2$\sqrt{2}$×$6\sqrt{2}×sinθ$=12$\sqrt{3}$,
解得sinθ=$\frac{\sqrt{3}}{2}$,
∵0°≤θ≤90°,∴θ=60°.
∴AB和CD所成的角为60°.
故答案为:60°.
点评 本题考查两条异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=-sin(4x+$\frac{π}{4}$) | D. | f(x)=sin(4x+$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {4,6} | C. | {2,4,6} | D. | {1,2,3,4,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
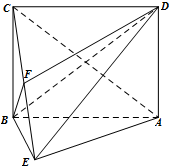 已知如图:四边形ABCD是矩形,BC⊥平面ABE,且AE=EB=BC=2,点F为CE上一点,且BF⊥平面ACE.
已知如图:四边形ABCD是矩形,BC⊥平面ABE,且AE=EB=BC=2,点F为CE上一点,且BF⊥平面ACE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com