
分析 (1)直接利用诱导公式化简求解即可.
(2)代入函数的解析式,利用同角三角函数基本关系式,化简求解即可.
(3)利用诱导公式化简求解即可.
解答 解:(1)$f(α)=\frac{{{{cos}^2}({\frac{π}{2}-α})sin({\frac{π}{2}+α})cot({\frac{π}{2}-α})}}{{sin({-π+α})tan({-α+3π})}}$
=$\frac{si{n}^{2}αcosαtanα}{sinαtanα}$=sinαcosα.
(2)$f(α)=sinαcosα=\frac{1}{8}$
则${({cosα-sinα})^2}=1-2sinαcosα=\frac{3}{4}$,
∴$\frac{π}{4}<α<\frac{π}{2}$,
∴sinα>cosα,
∴$cosα-sinα=-\frac{{\sqrt{3}}}{2}$
(3)$f({-\frac{31π}{3}})=sin({-\frac{31π}{3}})cos({-\frac{31π}{3}})=sin({-\frac{π}{3}})cos({-\frac{π}{3}})=-sin\frac{π}{3}cos\frac{π}{3}=-\frac{{\sqrt{3}}}{2}•\frac{1}{2}=-\frac{{\sqrt{3}}}{4}$
点评 本题考查诱导公式以及同角三角函数基本关系式的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {〔1,1〕} | B. | {〔-1,1〕} | C. | {〔1,0〕} | D. | {〔0,1〕} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
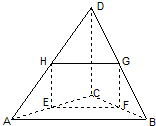 在空间四边形ABCD中,E,F,G,H分别是AC,BC,BD,DA的中点,若$AB=12\sqrt{2}$,$CD=4\sqrt{2}$,且四边形EFGH的面积为$12\sqrt{3}$,则AB和CD所成的角为60°.
在空间四边形ABCD中,E,F,G,H分别是AC,BC,BD,DA的中点,若$AB=12\sqrt{2}$,$CD=4\sqrt{2}$,且四边形EFGH的面积为$12\sqrt{3}$,则AB和CD所成的角为60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com