Question

17．若一个圆锥的母线长为4，高为2，则过这个圆锥的任意两条母线的截面面积的最大值是8．

Answer 1

分析 根据母线长为4，高为2，求出圆锥的底面半径．任意两条母线作截面，根据圆锥截图性质构造的三角形建立关系．利用基本不等式的性质求解．

解答 解：由题意：圆锥的母线长为4，高为2，
∴圆锥的底面半径r=$2\sqrt{3}$．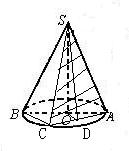
任意两条母线作截面（如图）ACS，
则CS=SA=4，△ACS是等腰三角形．
SD是△ACS的高，且是AC的中点．
设SD=h，AC=m，BC=n．
可得：h²+$\frac{1}{4}$m²=16
即4h²+m²=64，
那么：64=4h²+m²≥4mh，（当且仅当2h=m时取等号）
mh≤16．
则${S}_{△ACS}=\frac{1}{2}mh$=$\frac{1}{2}×16=8$
故答案为8．

点评 本题考查了圆锥截面图的面积的求法，构造等式关系．基本不等式的性质的思想．属于基础题．