
分析 (1)分别化简集合E,F,再根据集合的补集和交集的运算即可求出,
(2)对m进行分类讨论,即可求出m的取值范围.
解答 解:(1)m=4时,E={x||x-1|≥4}={x|x≤-3或x≥5},F={x|$\frac{10}{x+6}>1$}={x|(x-4)(x+6)<0}={x|-6<x<4}
∴(CRE)∩F={x|-3<x<5}∩{x|?6<x<4}={x|-3<x<4}.
(2)∵E={x||x-1|≥m},①m≤0时,E=R,E∩F=F≠∅,不满足条件
②m>0时,E={x|x≤1-m或x≥1+m},由E∩F=∅,F={x|-6<x<4},
∴$\left\{\begin{array}{l}1-m≤-6\\ 1+m≥4\\ m>0\end{array}\right.$解得m≥7,
∴综上,实数m的取值范围为m≥7.
点评 本题考查集合的交集、并集、补集的定义并用定义解决简单的集合运算.


科目:高中数学 来源: 题型:选择题
| A. | β=90°+α | B. | α+β=180° | C. | α=90°+β | D. | α+β=90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
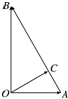 如图所示,已知∠B=30°,∠AOB=90°,点C在AB上,OC⊥AB,点D为OB中点,OC与AD相交点H,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OH}$,则$\overrightarrow{OH}$等于$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{1}{5}$$\overrightarrow{OB}$.
如图所示,已知∠B=30°,∠AOB=90°,点C在AB上,OC⊥AB,点D为OB中点,OC与AD相交点H,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OH}$,则$\overrightarrow{OH}$等于$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{1}{5}$$\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {〔1,1〕} | B. | {〔-1,1〕} | C. | {〔1,0〕} | D. | {〔0,1〕} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com