
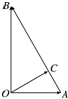
 如图所示,已知∠B=30°,∠AOB=90°,点C在AB上,OC⊥AB,点D为OB中点,OC与AD相交点H,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OH}$,则$\overrightarrow{OH}$等于$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{1}{5}$$\overrightarrow{OB}$.
如图所示,已知∠B=30°,∠AOB=90°,点C在AB上,OC⊥AB,点D为OB中点,OC与AD相交点H,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OH}$,则$\overrightarrow{OH}$等于$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{1}{5}$$\overrightarrow{OB}$. 分析 建立平面直角坐标系,求出点H的坐标,写出向量$\overrightarrow{OH}$,再用向量$\overrightarrow{OA}$、$\overrightarrow{OB}$表示出$\overrightarrow{OH}$即可.
解答 解:建立平面直角坐标系,如图所示,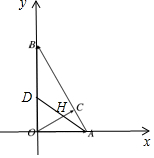
设OA=1,则OB=$\sqrt{3}$,AB=2,AC=$\frac{1}{2}$;
∴O(0,0),A(1,0),B(0,$\sqrt{3}$),D(0,$\frac{\sqrt{3}}{2}$),C($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$),
又直线OC的方程为y=$\frac{\sqrt{3}}{3}$x,AD的方程为x+$\frac{2y}{\sqrt{3}}$=1,
两方程联立,解得x=$\frac{3}{5}$,y=$\frac{\sqrt{3}}{5}$,
∴$\overrightarrow{OH}$=($\frac{3}{5}$,$\frac{\sqrt{3}}{5}$),
又$\overrightarrow{OA}$=(1,0),$\overrightarrow{OB}$=(0,$\sqrt{3}$);
∴$\overrightarrow{OH}$=$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{1}{5}$$\overrightarrow{OB}$.
故答案为:$\frac{3}{5}\overrightarrow{OA}+\frac{1}{5}\overrightarrow{OB}$.
点评 本题考查了平面向量的应用问题,解题时应建立适当的坐标系,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | 2 | C. | -2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x2≥1,则x≥1 | B. | 若x≥1,则x2≥1 | C. | 若x>1,则x2>1 | D. | 若x<1,则x2<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=-sin(4x+$\frac{π}{4}$) | D. | f(x)=sin(4x+$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{2}=1$ | B. | $\frac{x^2}{2}+\frac{y^2}{3}=1$ | C. | $\frac{x^2}{2}-\frac{y^2}{4}=1$ | D. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | 若“p或q”为真命题,则p,q中至少有一个为真命题 | |
| D. | 命题“若x=y,则cosx=cosy”的逆否命题为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三个点 | |
| B. | 两条直线 | |
| C. | 两两相交的三条直线,且有三个不同的交点 | |
| D. | 三条直线,其中一条直线与另外两条直线分别相交 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com