
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | 若“p或q”为真命题,则p,q中至少有一个为真命题 | |
| D. | 命题“若x=y,则cosx=cosy”的逆否命题为假命题 |
分析 写出原命题的否命题,可判断A;根据充要条件的定义,可判断B;根据复合命题真假判断的真值表,可判断C;判断原命题的真假,结合互为逆否的两个命题,真假性相同,可判断D.
解答 解:命题“若x2=1,则x=1”的否命题为:“若x2≠1,则x≠1”,故A错误;
“x2-5x-6=0”?“x=-1,或x=6”,
故“x=-1”是“x2-5x-6=0”的充分不必要条件,故B错误;
若“p或q”为真命题,则p,q中至少有一个为真命题,故C正确;
命题“若x=y,则cosx=cosy”为真命题,故其逆否命题为真命题,故D错误;
故选:C.
点评 本题以命题的真假判断与应用为载体,考查了四种命题,充要条件,复合命题等知识点,难度中档.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:填空题
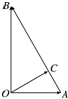 如图所示,已知∠B=30°,∠AOB=90°,点C在AB上,OC⊥AB,点D为OB中点,OC与AD相交点H,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OH}$,则$\overrightarrow{OH}$等于$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{1}{5}$$\overrightarrow{OB}$.
如图所示,已知∠B=30°,∠AOB=90°,点C在AB上,OC⊥AB,点D为OB中点,OC与AD相交点H,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OH}$,则$\overrightarrow{OH}$等于$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{1}{5}$$\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {〔1,1〕} | B. | {〔-1,1〕} | C. | {〔1,0〕} | D. | {〔0,1〕} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com