
���� ��1��������κ���f��x���������䷽�������κ�����ֵ�ɣ�
��2��������κ���f��x��=��x-sin�ȣ�2+$\frac{1}{4}$-sin2�ȣ�ͨ�������ĵ����ԣ��Ƴ�����������ʱsin�ȡ�$\frac{1}{2}$��������ʱsin�ȡ�-$\frac{1}{2}$����⼴�ɣ�
��3���жϺ�����[2��3]�ϵ��������������ֵ���õ�|f��x1��-f��x2��|����ֵ���Ƴ�����ʽ���t���ɣ�
��� �⣺��1�����κ���f��x��=x2-2sin��x+$\frac{1}{4}$����=$\frac{��}{6}$��
�ɵã�f��x��=x2-x+$\frac{1}{4}$=��x-$\frac{1}{2}$��2��[0��$\frac{9}{4}$]��
������ֵ��Ϊ��[0��$\frac{9}{4}$]��
��2����������κ���f��x��=x2-2sin��x+$\frac{1}{4}$=��x-sin�ȣ�2+$\frac{1}{4}$-sin2�ȣ�
����f��x��������[-$\frac{1}{2}$��$\frac{1}{2}}$]���ǵ���������
�ຯ��������ʱsin�ȡ�$\frac{1}{2}$��������ʱsin�ȡ�-$\frac{1}{2}$��$���Ԧȵ�ȡֵ����Ϊ[{\frac{��}{6}+2k�У�\left.{\frac{5��}{6}+2k��}]}\right.��[{\frac{7��}{6}+2k�У�\left.{\frac{11��}{6}+2k��}]}\right.��k��{Z}��$��
��3����Ϊ�Գ���x=sin�ȡ�1�����Ժ�����[2��3]�ϵ���������
�Ӷ�|f��x1��-f��x2��|��f��x��max-f��x��min
=f��3��-f��2����
=5-2sin�ȡ�2sin��t2+8t+5�����ԣ�1+t2��sin��+4t��0��������ȡ�R�������
��$\frac{-4t}{{1+{t^2}}}��sin�ȣ�\frac{-4t}{{1+{t^2}}}��{��sin�ȣ�_{min}}=-1$��
����t2-4t+1��0����t��ȡֵ��Χ��$[{\frac{{2-\sqrt{3}}}{2}}\right.��\left.{\frac{{2+\sqrt{3}}}{2}}]$��
���� ���⿼����κ�������ֵ������������������������˼���Լ�ת��˼���Ӧ�ã��������������


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
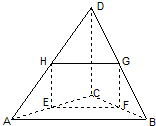 �ڿռ��ı���ABCD�У�E��F��G��H�ֱ���AC��BC��BD��DA���е㣬��$AB=12\sqrt{2}$��$CD=4\sqrt{2}$�����ı���EFGH�����Ϊ$12\sqrt{3}$����AB��CD���ɵĽ�Ϊ60�㣮
�ڿռ��ı���ABCD�У�E��F��G��H�ֱ���AC��BC��BD��DA���е㣬��$AB=12\sqrt{2}$��$CD=4\sqrt{2}$�����ı���EFGH�����Ϊ$12\sqrt{3}$����AB��CD���ɵĽ�Ϊ60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���Ϸ� | B�� | ���·� | C�� | ���Ϸ� | D�� | ���·� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -$\frac{1}{2}$ | C�� | $\frac{1}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {0} | B�� | {1} | C�� | {0��1} | D�� | {0��1��2��3��4} |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com