
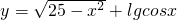 ;
;
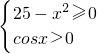 解得
解得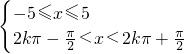
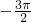 )∪(
)∪( )∪(
)∪( ,5]
,5] sinx-cosx>0 (*)
sinx-cosx>0 (*) sinx>0即cos(x+
sinx>0即cos(x+ )>0,又0≤x<π,所以
)>0,又0≤x<π,所以 <x+
<x+ <
< 故x∈[0,
故x∈[0, )
) sinx>0,即
sinx>0,即 cosx+sinx<0,可转化为sin(x+
cosx+sinx<0,可转化为sin(x+ )<0
)<0 <
< ,故x∈(
,故x∈( ,π)
,π) )∪(
)∪( ,π)
,π)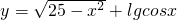 的定义域是[-5,
的定义域是[-5,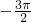 )∪(
)∪( )∪(
)∪( ,5]
,5] 的定义域是[0,
的定义域是[0, )∪(
)∪( ,π)
,π)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com