Question

4．已知△ABC是边长为1的正三角形，动点M在平面ABC内，若$\overrightarrow{AM}•\overrightarrow{AB}＜0$，$|\overrightarrow{CM}|=1$，则$\overrightarrow{CM}•\overrightarrow{AB}$的取值范围是[-1，-$\frac{1}{2}$）．

Answer 1

分析 以以AB的中点为坐标原点，AB所在直线为x轴，建立如图的直角坐标系，求出点的坐标以及相应向量的坐标，运用向量的数量积的坐标表示和向量模的公式，结合圆的性质，条件即可得到计算得到．

解答 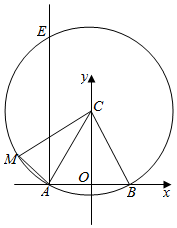解：以AB的中点为坐标原点，AB所在直线为x轴，建立如图的直角坐标系，
则A（-$\frac{1}{2}$，0），B（$\frac{1}{2}$，0），C（0，$\frac{\sqrt{3}}{2}$），设M（x，y），
由|$\overrightarrow{CM}$|=1，可得x²+（y-$\frac{\sqrt{3}}{2}$）²=1，
即有-1≤x≤1，①
又$\overrightarrow{AM}$=（x+$\frac{1}{2}$，y），$\overrightarrow{AB}$=（1，0），$\overrightarrow{CM}$=（x，y-$\frac{\sqrt{3}}{2}$）．
由$\overrightarrow{AM}•\overrightarrow{AB}＜0$，可得x+$\frac{1}{2}$＜0，
即有x＜-$\frac{1}{2}$，②
由①②可得-1≤x＜-$\frac{1}{2}$．
则$\overrightarrow{CM}•\overrightarrow{AB}$=x×1+（y-$\frac{\sqrt{3}}{2}$）×0=x，
则所求范围为[-1，-$\frac{1}{2}$）．
故答案为：[-1，-$\frac{1}{2}$）

点评 本题考查向量的数量积的坐标表示和向量模的公式，同时考查圆的性质和不等式的性质，利用数形结合以及利用坐标法是解决本题的关键．属于中档题．