
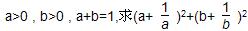 的最小值。
的最小值。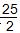
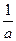 )2+(b+
)2+(b+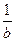 )2=a2+b2+
)2=a2+b2+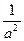 +
+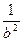 +4≥2ab+
+4≥2ab+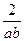 +4≥4
+4≥4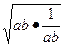 +4=8,
+4=8,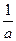 )2+(b+
)2+(b+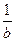 )2的最小值是8.
)2的最小值是8.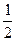 ,第二次等号成立的条件是ab=
,第二次等号成立的条件是ab=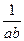 ,显然,这两个条件是不能同时成立的。因此,8不是最小值。
,显然,这两个条件是不能同时成立的。因此,8不是最小值。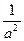 +
+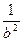 +4="(" a2+b2)+(
+4="(" a2+b2)+(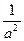 +
+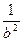 )+4=[(a+b)2-2ab]+[(
)+4=[(a+b)2-2ab]+[(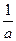 +
+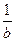 )2-
)2-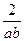 ]+4= (1-2ab)(1+
]+4= (1-2ab)(1+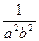 )+4,
)+4, )2=
)2=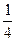 得:1-2ab≥1-
得:1-2ab≥1-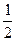 =
=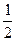 , 且
, 且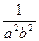 ≥16,1+
≥16,1+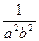 ≥17,
≥17,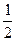 ×17+4=
×17+4=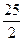 (当且仅当a=b=
(当且仅当a=b=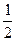 时,等号成立),
时,等号成立),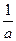 )2 + (b +
)2 + (b + 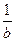 )2的最小值是
)2的最小值是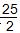 。
。

科目:高中数学 来源:不详 题型:解答题
 ,g(x)=
,g(x)= .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (单位:cm
(单位:cm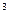 /s)与管道半径
/s)与管道半径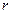 (单位:cm)的四次方成正比.
(单位:cm)的四次方成正比.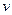 关于管道半径
关于管道半径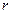 的函数解析式;
的函数解析式;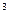 /s,求该气体通过半
/s,求该气体通过半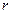 的管道时,其流量速率
的管道时,其流量速率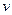 的表达式;
的表达式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (dB)由公式
(dB)由公式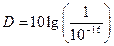 给出,其中
给出,其中 为声强(W/cm
为声强(W/cm ).声强小于
).声强小于 W/cm
W/cm 时,人听不见声音.求:
时,人听不见声音.求: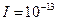 W/cm
W/cm )的声压级;
)的声压级; W/cm
W/cm )的声压级(精确到1dB);
)的声压级(精确到1dB);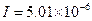 W/cm
W/cm )的声压级(精确到1dB).
)的声压级(精确到1dB).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com