
| A. | -$\frac{3}{2}$ | B. | -$\frac{5}{2}$ | C. | -4 | D. | 4 |
分析 若f(x)=f($\frac{x+1}{2x+4}$),则x=$\frac{x+1}{2x+4}$或-x=$\frac{x+1}{2x+4}$,利用韦达定理,可得答案.
解答 解:∵f(x)是连续的偶函数,且当x>0时是单调函数,
若f(x)=f($\frac{x+1}{2x+4}$),则
x=$\frac{x+1}{2x+4}$或-x=$\frac{x+1}{2x+4}$,
即2x2+3x-1=0或2x2+5x+1=0,
故${x}_{1}+{x}_{2}=-\frac{3}{2}$,${x}_{3}+{x}_{4}=-\frac{5}{2}$,
则满足f(x)=f($\frac{x+1}{2x+4}$)的所有x之和为-4,
故选:C.
点评 本题考查的知识点是函数的单调性,函数的奇偶性,抽象函数的应用,难度中档.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{2\sqrt{7}}{7}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《九章算术》是我国古代的数学巨著,其卷第五“商功”有如下的问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”意思为:“今有底面为矩形的屋脊形状的多面体(如图)”,下底面宽AD=3丈,长AB=4丈,上棱EF=2丈,EF∥平面ABCD.EF与平面ABCD的距离为1丈,问它的体积是( )
《九章算术》是我国古代的数学巨著,其卷第五“商功”有如下的问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”意思为:“今有底面为矩形的屋脊形状的多面体(如图)”,下底面宽AD=3丈,长AB=4丈,上棱EF=2丈,EF∥平面ABCD.EF与平面ABCD的距离为1丈,问它的体积是( )| A. | 4立方丈 | B. | 5立方丈 | C. | 6立方丈 | D. | 8立方丈 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知关于x的二次函数f(x)=ax2-4bx+1.
已知关于x的二次函数f(x)=ax2-4bx+1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}}$ | B. | y=a${\;}^{lo{g}_{a}x}$ | C. | y=$\frac{{x}^{2}}{x}$ | D. | y=$\root{3}{{x}^{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
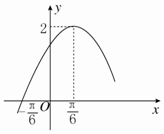 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆C上异于顶点的任一点P作圆O:x2+y2=b2的两条切线,切点分别为A,B,若直线AB与x,y轴分别交于M,N两点,则$\frac{{b}^{2}}{|OM{|}^{2}}$+$\frac{{a}^{2}}{|ON{|}^{2}}$的值为( )
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆C上异于顶点的任一点P作圆O:x2+y2=b2的两条切线,切点分别为A,B,若直线AB与x,y轴分别交于M,N两点,则$\frac{{b}^{2}}{|OM{|}^{2}}$+$\frac{{a}^{2}}{|ON{|}^{2}}$的值为( )| A. | 1 | B. | $\frac{5}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com