
 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆C上异于顶点的任一点P作圆O:x2+y2=b2的两条切线,切点分别为A,B,若直线AB与x,y轴分别交于M,N两点,则$\frac{{b}^{2}}{|OM{|}^{2}}$+$\frac{{a}^{2}}{|ON{|}^{2}}$的值为( )
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆C上异于顶点的任一点P作圆O:x2+y2=b2的两条切线,切点分别为A,B,若直线AB与x,y轴分别交于M,N两点,则$\frac{{b}^{2}}{|OM{|}^{2}}$+$\frac{{a}^{2}}{|ON{|}^{2}}$的值为( )| A. | 1 | B. | $\frac{5}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
分析 由椭圆的离心率结合隐含条件求得$\frac{{b}^{2}}{{a}^{2}}=\frac{4}{3}$,设A(xA,yA ),B (xB,yB ),则可得切线PA、PB的方程,即可得到A,B 是xP•x+yP•y=b2 和圆x2+y2=b2 的交点,求出点M($\frac{{b}^{2}}{{x}_{P}}$,0),N(0,$\frac{{b}^{2}}{{y}_{P}}$),从而得到$\frac{{a}^{2}}{|ON{|}^{2}}+\frac{{b}^{2}}{|OM{|}^{2}}$=$\frac{{a}^{2}{{y}_{P}}^{2}}{{b}^{4}}+\frac{{a}^{2}{{x}_{P}}^{2}}{{b}^{4}}$=($\frac{{{x}_{P}}^{2}}{{a}^{2}}+\frac{{{y}_{P}}^{2}}{{b}^{2}}$)•$\frac{{b}^{2}}{{a}^{2}}$=$\frac{{b}^{2}}{{a}^{2}}$,答案可求.
解答 解:$e=\frac{c}{a}=\frac{1}{2}$,∴$\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{4}$,得$\frac{{b}^{2}}{{a}^{2}}=\frac{4}{3}$.
设A(xA,yA ),B (xB,yB ),则切线PA、PB的方程分别为 xA•x+yA•y=b2,xB•x+yB•y=b2.
由于点P 是切线PA、PB的交点,
∴点P的坐标满足切线PA的方程,也满足切线PB的方程.
∴A,B 是xP•x+yP•y=b2 和圆x2+y2=b2 的交点,故点M($\frac{{b}^{2}}{{x}_{P}}$,0),N(0,$\frac{{b}^{2}}{{y}_{P}}$).
又$\frac{{{x}_{P}}^{2}}{{a}^{2}}+\frac{{{y}_{P}}^{2}}{{b}^{2}}=1$,
∴$\frac{{a}^{2}}{|ON{|}^{2}}+\frac{{b}^{2}}{|OM{|}^{2}}$=$\frac{{a}^{2}{{y}_{P}}^{2}}{{b}^{4}}+\frac{{a}^{2}{{x}_{P}}^{2}}{{b}^{4}}$=($\frac{{{x}_{P}}^{2}}{{a}^{2}}+\frac{{{y}_{P}}^{2}}{{b}^{2}}$)•$\frac{{b}^{2}}{{a}^{2}}$=$\frac{{b}^{2}}{{a}^{2}}$=$\frac{4}{3}$.
故选:D.
点评 本题考查椭圆的标准方程,以及简单性质的应用,得到故A,B 是xP•x+yP•y=b2 和圆x2+y2=b2 的交点,是解题的难点和关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | -$\frac{5}{2}$ | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {3,4} | C. | {5,6,7} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
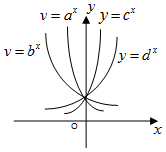 指数函数y=ax、y=bx、y=cx、y=dx在同一坐标系中的图象如图所示,则a,b,c,d与1的大小关系为( )
指数函数y=ax、y=bx、y=cx、y=dx在同一坐标系中的图象如图所示,则a,b,c,d与1的大小关系为( )| A. | 0<a<b<1<c<d | B. | 0<a<b<1<d<c | C. | 1<a<b<c<d | D. | 0<b<a<1<d<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com