
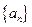 满足
满足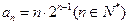 .是否存在等差数列
.是否存在等差数列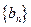 ,使得数列
,使得数列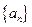 与
与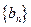 满足
满足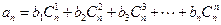 对一切正整数
对一切正整数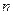 成立? 证明你的结论.
成立? 证明你的结论.  ,有
,有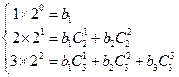 ,即
,即 ,
, . 由此猜想:
. 由此猜想: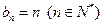 . ----------------4分
. ----------------4分  .
.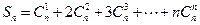
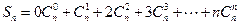
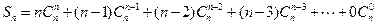 ------------8分
------------8分 ------------10分
------------10分 ,即
,即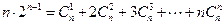 . ------------12分
. ------------12分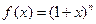 ,
,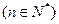 ,由二项式定理,知
,由二项式定理,知 , -------------------8分
, -------------------8分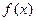 求导,得
求导,得 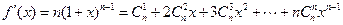 ---10分
---10分 ,即得
,即得 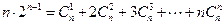 . -------------------12分
. -------------------12分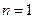 时,
时,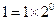 成立. --------------------------5分
成立. --------------------------5分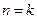 时等式成立,即
时等式成立,即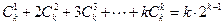 .
. 时,
时, 
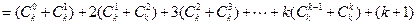
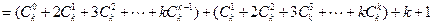




 时,等式也成立.
时,等式也成立.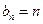 ,使得
,使得 对一切
对一切 成立. ---------------------12分
成立. ---------------------12分

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源:不详 题型:解答题
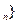 中,a
中,a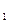 =5且a
=5且a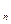 =3a
=3a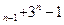 (n≥2)
(n≥2)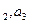 的值.
的值.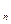 =
=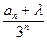 ,是否存在实数λ,使数列{b
,是否存在实数λ,使数列{b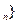 为等差数列,若存在请求其通项b
为等差数列,若存在请求其通项b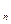 ,若不存在请说明理由.
,若不存在请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 )
)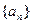 生成的数列
生成的数列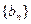 满足对任意的
满足对任意的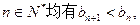 其中
其中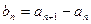 ,则称数列
,则称数列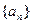 为“Z数列”。
为“Z数列”。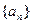 中,已知
中,已知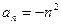 ,试判断数列
,试判断数列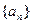 是否为“Z数列”;
是否为“Z数列”; II)若数列
II)若数列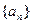 是“Z数列”,
是“Z数列”,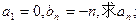
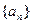 是“Z数列”,设
是“Z数列”,设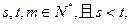 求证
求证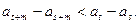
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com