
(Ⅰ)当a=1时,设g(x)=f(x)+cx(c∈R),且函数y=g(x)的图像有与x轴平行的切线,求c的取值范围;
(Ⅱ)当a>0时,若f(x)在区间[-1,2]上的最大值为27,最小值办-13,讨论函数h(x)=|f(x)-13|(x∈[0,2])的单调性.
(Ⅰ)解:(1)当a=l时,f(x)=2x3-9x2+b,
∴g(x)=2x3-9x2+cx+b(b、c∈R)
又g′(x)=6x2-18x+c,且y=g(x)的图像有与x轴平行的切线,
∴g′(x)=0有解,即方程6x2-18x+c=0有解
∴△=182-4×6×c≥0,即:c≤![]()
(Ⅱ)据题知f′(x)=6ax2-18ax=6ax(x-3),令f′(x)=0,
在[-1,2]解为x=0,f(0)=b
当a>0时,有
x | [-1,0] | 0 | (0,2] |
f′(x) | + | 0 | - |
f(x) |
| 极大 |
|
则f(0)必为最大值,f(0)=b=27,而
fmin(x)=min{f(-1),f(2)},
又f(-1)=-2a-9a+27=-11a+27,
f(2)=16a-36a+27=-20a+27,
∴f(2)<f(-1),f(2)为最小值,即
f(2)=-20a+27=-13,解得a=2,
从而f(x)=4x3-18x2+27
又f(x)-13=4x3-18x2+14=4x3-4x2+14
=4x2(x-1)-14(x+1)(x-1)
=2(x-1)(2x2-7x-7)
即:h(x)=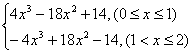
易知函数h(x)在区间[0,1]上是单调减函数,在区间(1,2]上是单调增函数.


科目:高中数学 来源: 题型:
| 2-x | x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ax+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com