Question

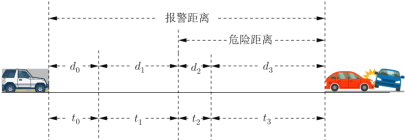
【题目】汽车智能辅助驾驶已得到广泛应用，其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离（并结合车速转化为所需时间），当此距离等于报警距离时就开始报警提醒，等于危险距离时就自动刹车，某种算法（如下图所示）将报警时间划分为4段，分别为准备时间、人的反应时间、系统反应时间、制动时间，相应的距离分别为、、、，当车速为（米/秒），且时，通过大数据统计分析得到下表（其中系数随地面湿滑成都等路面情况而变化，）.

阶段	0、准备	1、人的反应	2、系统反应	3、制动
时间		秒	秒
距离	米			米

（1）请写出报警距离（米）与车速（米/秒）之间的函数关系式，并求时，若汽车达到报警距离时人和系统均不采取任何制动措施，仍以此速度行驶，则汽车撞上固定障碍物的最短时间（精确到0.1秒）；

（2）若要求汽车不论在何种路面情况下行驶，报警距离均小于80米，则汽车的行驶速度应限制在多少米/秒以下？合多少千米/小时？

Answer 1

【答案】（1），最短时间秒（2）汽车的行驶速度应限制在米/秒，合72千米/小时

【解析】

（1）根据题意，得到，结合题中数据，即可得出函数关系式；再由，得到汽车撞上固定障碍物的最短时间，根据基本不等式，即可求出最值；

（2）根据题意，得到当时，报警距离最大，推出，求解即可得出结果.

（1）由题意：报警距离，

当时，，

则汽车撞上固定障碍物的最短时间为：秒；

（2）由题意可得：，因为，

所以当时，报警距离最大，

因此，只需：，解得：，所以汽车的行驶速度应限制在米/秒，合72千米/小时.