
【题目】如图,在平面四边形ABCD中,DA⊥AB,
 DE=1,EC=
DE=1,EC=![]() ,EA=2,
,EA=2,
∠ADC=![]() ,∠BEC=
,∠BEC=![]() .
.
(Ⅰ)求sin∠CED的值;
(Ⅱ)求BE的长.
【答案】(1) sin∠CED=![]() ;(2) BE=4
;(2) BE=4![]() .
.
【解析】试题分析:(1)由余弦定理得,EC2=CD2+DE2-2CD·DE·cos∠EDC,解得CD=2;在△CDE中,由正弦定理得sin∠CED=![]() ;(2)cos ∠AEB=cos
;(2)cos ∠AEB=cos ![]() -α,cos α=
-α,cos α=![]() =
=![]() Rt△EAB中,cos∠AEB=
Rt△EAB中,cos∠AEB=![]() ,BE=4
,BE=4![]() 。
。
(Ⅰ)在△CDE中,由余弦定理得,EC2=CD2+DE2-2CD·DE·cos∠EDC.
由题设知,7=CD2+1+CD,即CD2+CD-6=0.解得CD=2(CD=-3舍去).
在△CDE中,由正弦定理得, ![]() ,
,
于是sin α=![]() ,即sin∠CED=
,即sin∠CED=![]() .
.
(Ⅱ)由题设知,0<α<![]() ,于是由(1)知,cos α=
,于是由(1)知,cos α=![]() =
=![]() .
.
而∠AEB=![]() -α,所以cos ∠AEB=cos
-α,所以cos ∠AEB=cos ![]() -α =cos
-α =cos ![]() cos α+sin
cos α+sin ![]() sin α=-
sin α=-![]() cos α+
cos α+![]() sin α=
sin α=![]() .
.
在Rt△EAB中,cos∠AEB=![]() =
=![]() ,故BE=4
,故BE=4![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上、下顶点分别是
,上、下顶点分别是![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]() ,且
,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年中国(云南赛区)三对三篮球联赛在昆明市体育局的大力支持下,圆满顺利结束.组织方统计了来自![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队 |
|
|
|
|
|
平均身高 | 170 | 174 | 176 | 181 | 179 |
平均得分 | 62 | 64 | 66 | 70 | 68 |
(2)若![]() 队平均身高为
队平均身高为![]()
![]() ,根据(1)中所求得的回归方程,预测
,根据(1)中所求得的回归方程,预测![]() 队的平均得分.(精确到个位)
队的平均得分.(精确到个位)
注:回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为
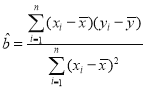 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b是函数f(x)=x2﹣px+q(p>0,q>0)的两个不同的零点,且a,b,﹣2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于;点A坐标(p,q),曲线C方程:y= ![]() ,直线l过A点,且和曲线C只有一个交点,则直线l的斜率取值范围为 .
,直线l过A点,且和曲线C只有一个交点,则直线l的斜率取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,设边a,b,c所对的角为A,B,C,且A,B,C都不是直角,(bc﹣8)cosA+accosB=a2﹣b2 .
(1)若b+c=5,求b,c的值;
(2)若 ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差为d的等差数列{an}中,已知a1=10,5a1a3=(2a2+2)2 .
(1)求d和an的值;
(2)若d<0,求|a1|+|a2|+|a3|+…+|a2021|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com