
(本小题满分14分)在平面直角坐标系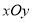 中,已知圆
中,已知圆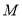 过坐标原点O且圆心在曲线
过坐标原点O且圆心在曲线 上.
上.
(Ⅰ)若圆M分别与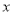 轴、
轴、 轴交于点
轴交于点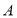 、
、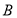 (不同于原点O),求证:
(不同于原点O),求证: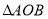 的面积为定值;
的面积为定值;
(Ⅱ)设直线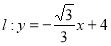 与圆M 交于不同的两点C,D,且
与圆M 交于不同的两点C,D,且 ,求圆M的方程;
,求圆M的方程;
(Ⅲ)设直线 与(Ⅱ)中所求圆M交于点
与(Ⅱ)中所求圆M交于点 、
、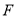 ,
, 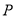 为直线
为直线 上的动点,直线
上的动点,直线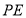 ,
, 与圆M的另一个交点分别为
与圆M的另一个交点分别为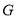 ,
,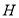 ,求证:直线
,求证:直线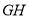 过定点.
过定点.
(Ⅰ)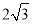 ;(Ⅱ)
;(Ⅱ)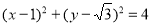 ;(Ⅲ)
;(Ⅲ)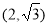 或
或 .
.
【解析】
试题分析:(Ⅰ)由题意可设圆M的方程为 ,求出圆M分别与x轴、y轴交于点A、B的坐标,利用面积公式,可得:△AOB的面积为定值;
,求出圆M分别与x轴、y轴交于点A、B的坐标,利用面积公式,可得:△AOB的面积为定值;
(Ⅱ)由|OC|=|OD|,知OM⊥l,解得t=±1,再验证,即可求圆M的方程;
(Ⅲ)设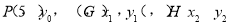 ,整理得
,整理得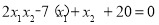 .①设直线GH的方程为
.①设直线GH的方程为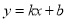 ,代入
,代入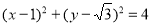 ,利用韦达定理,确定直线方程,即可得出结论.
,利用韦达定理,确定直线方程,即可得出结论.
试题解析:(Ⅰ)由题意可设圆M的方程为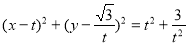 ,
,
即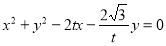 .
.
令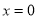 ,得
,得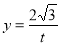 ;令
;令 ,得
,得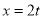 .
.
 (定值).
(定值).
(Ⅱ)由 ,知
,知 .
.
所以 ,解得
,解得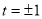 .
.
当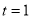 时,圆心M
时,圆心M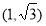 到直线
到直线 的距离
的距离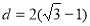 小于半径,符合题意;
小于半径,符合题意;
当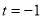 时,圆心M
时,圆心M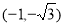 到直线
到直线 的距离
的距离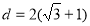 大于半径,不符合题意.
大于半径,不符合题意.
所以,所求圆M的方程为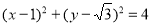 .
.
(Ⅲ)设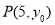 ,
, ,
,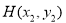 ,又知
,又知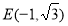 ,
,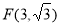 ,
,
所以 ,
,
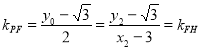 .
.
因为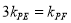 ,所以
,所以 .
.
将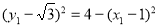 ,
,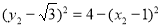 代入上式,
代入上式,
整理得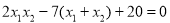 . ①
. ①
设直线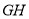 的方程为
的方程为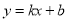 ,代入
,代入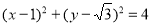 ,
,
整理得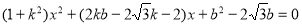 .
.
所以 ,
, .
.
代入①式,并整理得 ,
,
即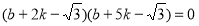 ,
,
解得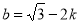 或
或 .
.
当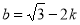 时,直线
时,直线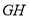 的方程为
的方程为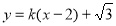 ,过定点
,过定点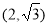 ;
;
当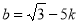 时,直线
时,直线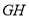 的方程为
的方程为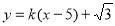 ,过定点
,过定点
考点:圆的方程;直线与圆的位置关系;分析思考能力和计算能力.


科目:高中数学 来源:2014-2015学年安徽省蚌埠市高一上学期期中考试数学试卷(解析版) 题型:选择题
将函数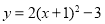 的图像向右平移1个单位长度,再向上平移3个单位长度,所得的图像所对应的函数解析式为( )
的图像向右平移1个单位长度,再向上平移3个单位长度,所得的图像所对应的函数解析式为( )
A.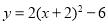 B.
B.
C.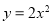 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二上学期期中考试理科数学试卷(解析版) 题型:选择题
直线 不经过坐标原点O,且与椭圆
不经过坐标原点O,且与椭圆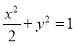 交于A、B两点,M是线段AB的中点.那么,直线AB与直线OM的斜率之积为 ( )
交于A、B两点,M是线段AB的中点.那么,直线AB与直线OM的斜率之积为 ( )
A.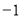 B.1 C.
B.1 C.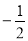 D.2
D.2
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)在一个盒子中装有6枝圆珠笔,其中3枝一等品,2枝二等品和1枝三等品,从中任取3枝,
求:(Ⅰ)取出的3枝中恰有1枝一等品的概率;
(Ⅱ)取出的3枝中一、二、三等品各一枝的概率;
(Ⅲ)取出的3枝中没有三等品的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
下表是一位母亲给儿子作的成长记录:
年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/cm | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
根据以上样本数据,她建立了身高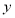 (cm)与年龄x(周岁)的线性回归方程为
(cm)与年龄x(周岁)的线性回归方程为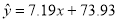 ,给出下列结论:
,给出下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本的中心点(42,117.1);
③儿子10岁时的身高是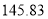 cm;
cm;
④儿子年龄增加1周岁,身高约增加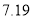 cm.
cm.
其中,正确结论的个数是
A.1 B.2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com