
分析 (1)如图所示,根据题意确定出|AB|与|OA|的长,利用勾股定理求出|OB|的长,进而确定出a与b的值,即可确定出椭圆M方程;
(2)设A(x1,y1),B(x2,y2),根据线段AB的垂直平分线经过点(0,$\frac{1}{2}$),得到直线AB斜率存在,分两种情况考虑:若直线AB斜率为0,得到线段AB的垂直平分线为y轴,表示出三角形AOB面积,利用基本不等式求出面积的最大值;直线AB斜率不为0,设直线AB为y=kx+t,与椭圆方程联立,消去y得到关于x的一元二次方程,利用根与系数的关系表示出x1+x2,进而表示出$\frac{1}{2}$(x1+x2)与$\frac{1}{2}$(y1+y2),根据斜率计算方法列出关系式,整理后记作①,再利用点到直线的距离公式表示出原点到直线的距离d,以及|AB|的长,进而表示出三角形AOB面积,求出三角形AOB面积的最大值即可.
解答 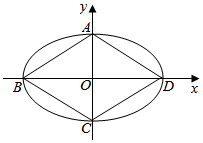 解:(1)∵椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点恰好是一边长为2,一内角为60°的菱形的四个顶点,
解:(1)∵椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的四个顶点恰好是一边长为2,一内角为60°的菱形的四个顶点,
∴四边形ABCD是菱形,且|AB|=2,∠ABC=60°,
∴△AOB为直角三角形,|OA|=1,
根据勾股定理得:|OB|=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴a=$\sqrt{3}$,b=1,
则椭圆方程为$\frac{{x}^{2}}{3}$+y2=1;
(2)设A(x1,y1),B(x2,y2),
∵线段AB的垂直平分线经过点(0,$\frac{1}{2}$),
∴直线AB斜率存在,
当直线AB斜率为0时,线段AB的垂直平分线是y轴,则有x1=-x2,y1=y2,
∴S△AOB=$\frac{1}{2}$•|2x1|•|y1|=|x1|•|y1|=|x1|•$\sqrt{1-\frac{{{x}_{1}}^{2}}{3}}$=$\sqrt{{{x}_{1}}^{2}(1-\frac{{{x}_{1}}^{2}}{3})}$=$\sqrt{\frac{1}{3}{{x}_{1}}^{2}(3-{{x}_{1}}^{2})}$,
∵$\sqrt{{{x}_{1}}^{2}(3-{{x}_{1}}^{2})}$≤$\frac{{{x}_{1}}^{2}+3-{{x}_{1}}^{2}}{2}$=$\frac{3}{2}$,
∴S△AOB≤$\frac{\sqrt{3}}{2}$,当且仅当|x1|=$\frac{\sqrt{6}}{2}$时,S△AOB的最大值是$\frac{\sqrt{3}}{2}$;
当直线AB的斜率不为0时,设直线AB为y=kx+t,
联立得:$\left\{\begin{array}{l}{\frac{{x}^{2}}{3}+{y}^{2}=1}\\{y=kx+t}\end{array}\right.$,
消去y得:(3k2+1)x2+6ktx+3t2-3=0,
当△=4(9k2+3-3t2)>0,即3k2+1>t2①,方程有两个不相等的实数根,
根据根与系数的关系得:x1+x2=-$\frac{6kt}{3{k}^{2}+1}$,即$\frac{1}{2}$(x1+x2)=-$\frac{3kt}{3{k}^{2}+1}$,
∴$\frac{1}{2}$(y1+y2)=$\frac{t}{3{k}^{2}+1}$,
∵$\frac{\frac{{y}_{1}+{y}_{2}}{2}+\frac{1}{2}}{0-\frac{{x}_{1}+{x}_{2}}{2}}$=$\frac{1}{k}$,
∴3k2+1=4t②,
代入①得:4t>t2,
解得:0<t<4,
∵原点到直线AB的距离d=$\frac{|t|}{\sqrt{1+{k}^{2}}}$,|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{4(9{k}^{2}+3-3{t}^{2})}}{3{k}^{2}+1}$,
∴S△AOB=$\frac{1}{2}$•|AB|•d=$\frac{1}{2}$$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{4(9{k}^{2}+3-3{t}^{2})}}{3{k}^{2}+1}$•$\frac{|t|}{\sqrt{1+{k}^{2}}}$=$\frac{1}{4}$$\sqrt{3(4t-{t}^{2})}$,
∵0<t<4,∴当t=2,即k=±$\sqrt{\frac{7}{3}}$时,S△AOB取得最大值$\frac{\sqrt{3}}{2}$,
综上,S△AOB的最大值是$\frac{\sqrt{3}}{2}$.
点评 此题考查了直线与圆锥曲线的关系,涉及的知识有:椭圆的简单性质,勾股定理,等边三角形的性质,根与系数的关系,直线与椭圆相交的性质,点到直线的距离公式,以及基本不等式的运用,熟练掌握性质及公式是解本题的关键.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
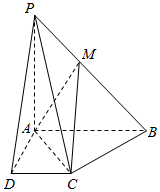 如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2.
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com