
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求函数![]() 的单调区间;
的单调区间;
(Ⅲ)用![]() 表示
表示![]() ,
,![]() 中的较大者,记函数
中的较大者,记函数![]() .若函数
.若函数![]() 在
在![]() 内恰有2个零点,求实数
内恰有2个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)单调递增区间为
(Ⅱ)单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .(Ⅲ)
.(Ⅲ)![]()
【解析】
(Ⅰ)当![]() 时,
时,![]() ,求出切点坐标和切线斜率,通过直线的点斜式方程可求出切线方程。
,求出切点坐标和切线斜率,通过直线的点斜式方程可求出切线方程。
(Ⅱ)对函数![]() 求导,由导函数的正负求单调性,同时注意对参数的讨论。
求导,由导函数的正负求单调性,同时注意对参数的讨论。
(Ⅲ)由题可知函数![]() 在
在![]() 内单调递减,当
内单调递减,当![]() 时,
时,![]() ,则函数
,则函数![]() 无零点。再对当
无零点。再对当![]() ,当
,当![]() 的情况进行分类讨论,最后得到答案。
的情况进行分类讨论,最后得到答案。
解:(Ⅰ)当![]() 时,
时,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即切线方程为![]() .
.
(Ⅱ)由已知得,![]()
(1)当![]() 时,
时,![]() ,
,
∴函数![]() 在
在![]() 内单调递增.
内单调递增.
(2)当![]() 时,令
时,令![]() ,
,
解得![]() 或
或![]() .
.
由![]() ,解得
,解得![]() 或
或![]() ,
,
由![]() ,解得
,解得![]() .
.
∴函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .
.
(Ⅲ)∵函数![]() 的定义域为
的定义域为![]() .
.
∴![]() . ∴函数
. ∴函数![]() 在
在![]() 内单调递减.
内单调递减.
(1)当![]() 时,
时,![]() ,
,
依题意,![]() ,则函数
,则函数![]() 无零点.
无零点.
(2)当![]() 时,
时,![]() ,
,![]() ,
,
①若![]() ,即
,即![]() ,则
,则![]() 是函数
是函数![]() 的一个零点;
的一个零点;
②若![]() ,即
,即![]() ,则
,则![]() 不是函数
不是函数![]() 的零点;
的零点;
(3)当![]() 时,
时,![]() ,只需考虑函数
,只需考虑函数![]() 在
在![]() )内零点的情况.
)内零点的情况.
∵![]() ,
,
①当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 内单调递增.
内单调递增.
又![]() ,
,
(ⅰ)当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 内无零点;
内无零点;
(ⅱ)当![]() 时,
时,![]() ,
,
又![]() ,
,
此时函数![]() 在
在![]() 内恰有一个零点;
内恰有一个零点;
②当![]() 时,由(Ⅱ)知,函数
时,由(Ⅱ)知,函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增.
内单调递增.
∵![]() ,
,
![]() ,
,
∴此时函数![]() 在
在![]() 内恰有一个零点.
内恰有一个零点.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥![]() 中,
中,![]() 与
与![]() 都是边长为2的等边三角形,
都是边长为2的等边三角形,![]() 、
、![]() 、
、![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 、
、![]() 、
、![]() 的中点.
的中点.
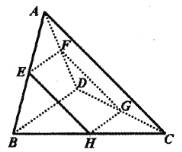
(1)证明:四边形![]() 为矩形;
为矩形;
(2)若平面![]() 平面
平面![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
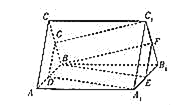
【题目】如图所示,三棱柱ABC﹣A1B1C1的侧棱垂直于底面,且底面是边长为2的正三角形,AA1=3,点D,E,F,G分别是所在棱的中点.
(Ⅰ)证明:平面BEF∥平面DA1C1;
(Ⅱ)求三棱柱ABC﹣A1B1C1夹在平面BEF和平面DA1C1之间的部分的体积.
附:台体的体积![]() ,其中S和S′分别是上、下底面面积,h是台体的高.
,其中S和S′分别是上、下底面面积,h是台体的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
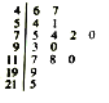
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.某环保人士从当地某年的AQI记录数据中,随机抽取了15天的AQI数据,用如图所示的茎叶图记录.根据该统计数据,估计此地该年空气质量为优或良的天数约为__________.(该年为366天)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的椭圆或双曲线的标准方程:
(1)椭圆的焦点在![]() 轴上,焦距为4,且经过点
轴上,焦距为4,且经过点![]() ;
;
(2)双曲线的焦点在![]() 轴上,右焦点为
轴上,右焦点为![]() ,过
,过![]() 作重直于
作重直于![]() 轴的直线交双曲线于
轴的直线交双曲线于![]() ,
,![]() 两点,且
两点,且![]() ,离心率为
,离心率为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动,组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后,学生会对问卷结果进行了统计,并将其中一个问题“是否知道垃圾分类方法(知道或不知道)”的调查结果统计如下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
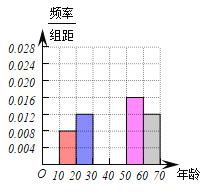
(1)求上表中的![]() 的值,并补全右图所示的的频率直方图;
的值,并补全右图所示的的频率直方图;
(2)在被调查的居民中,若从年龄在![]() 的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】苹果是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的富士苹果,各产地的包装规格相同,它们的批发价格(元/箱)和市场份额如下:
产地 |
|
|
|
|
|
批发价格 |
|
|
|
|
|
市场份额 |
|
|
|
|
|
市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.
(1)从该地批发市场销售的富士苹果中随机抽取一箱,求该箱苹果价格低于![]() 元的概率;
元的概率;
(2)按市场份额进行分层抽样,随机抽取![]() 箱富士苹果进行检验,
箱富士苹果进行检验,
①从产地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②从这![]() 箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
(3)由于受种植规模和苹果品质的影响,预计明年产地![]() 的市场份额将增加
的市场份额将增加![]() ,产地
,产地![]() 的市场份额将减少
的市场份额将减少![]() ,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱
,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱![]() 元,明年苹果的平均批发价为每箱
元,明年苹果的平均批发价为每箱![]() 元,比较
元,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() 、
、![]() ,椭圆的离心率为
,椭圆的离心率为![]() ,
,![]() 为椭圆上任意一点,
为椭圆上任意一点,![]() 的最大面积为
的最大面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() ,若
,若![]() 的内切圆面积为
的内切圆面积为![]() ,则求直线
,则求直线![]() 方程.
方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com