
【题目】如图,在空间四面体![]() 中,
中, ![]() ⊥平面
⊥平面![]() ,
,![]() ,且
,且![]() .
.

(1)证明:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求四面体![]() 体积的最大值,并求此时二面角
体积的最大值,并求此时二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() ,
,![]()
【解析】
(1)由勾股定理可得![]() ,由线面垂直的性质可得
,由线面垂直的性质可得![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 面
面![]() ,从而可得结果;(2)设
,从而可得结果;(2)设![]() ,则
,则![]() ,
,
由棱锥的体积公式求得棱锥的体积,利用导数可得体积的最大值;以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,利用向量垂直数量积为零列方程求得平面
轴,建立空间直角坐标系,利用向量垂直数量积为零列方程求得平面![]() 与平面
与平面![]() 的法向量,利用空间向量夹角余弦公式求解即可.
的法向量,利用空间向量夹角余弦公式求解即可.
(1) ,
,![]()
故![]() 即
即![]()
又![]()
![]()
由![]() 、
、![]() 得
得![]()
故有平面![]() ⊥平面
⊥平面![]()
(2)设![]() ,则
,则![]()
四面体![]() 的体积
的体积![]()
![]() ,故
,故![]() 在
在![]() 单增,在
单增,在![]() 单减
单减
易知![]() 时四面体
时四面体![]() 的体积
的体积![]() 最大,且最大值是
最大,且最大值是![]()
以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系
则![]()
设平面![]() 的法向量为
的法向量为![]() 则由
则由
取![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]()
同理可得平面![]() 的一个法向量
的一个法向量![]()
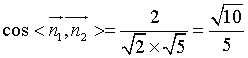
由于![]() 是锐二面角,故所求二面角的余弦值为
是锐二面角,故所求二面角的余弦值为![]()


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() 为常数).
为常数).
(1)若函数![]() 与函数
与函数![]() 在
在![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,证明:
,证明: ![]() ;
;
(3)若对任意![]() ,不等式恒
,不等式恒![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() 、
、![]() ,并且直线
,并且直线![]() 平分圆
平分圆![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)若过点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 有两个不同的交点
有两个不同的交点![]() 、
、![]() .
.
(i)求实数![]() 的取值范围;
的取值范围;
(ii)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现要完成下列三项抽样调查:①从![]() 罐奶粉中抽取
罐奶粉中抽取![]() 罐进行食品安全卫生检查;②高二年级有
罐进行食品安全卫生检查;②高二年级有![]() 名学生,为调查学生的学习情况抽取一个容量为
名学生,为调查学生的学习情况抽取一个容量为![]() 的样本;③从某社区
的样本;③从某社区![]() 户高收入家庭,
户高收入家庭,![]() 户中等收入家庭,
户中等收入家庭,![]() 户低收入家庭中选出
户低收入家庭中选出![]() 户进行消费水平调查.以下各调查方法较为合理的是( )
户进行消费水平调查.以下各调查方法较为合理的是( )
A.①系统抽样,②简单随机抽样,③分层抽样
B.①简单随机抽样,②分层抽样,③系统抽样
C.①分层抽样,②系统抽样,③简单随机抽样
D.①简单随机抽样,②系统抽样,③分层抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)设![]() 分别为
分别为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com