
【题目】已知函数![]() ,
,![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若对任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,在
时,在![]() 上,
上,![]() 是减函数,当
是减函数,当![]() 时,在
时,在![]() 上,
上,![]() 是减函数,在
是减函数,在![]() 上,
上,![]() 是增函数;(2)
是增函数;(2)![]()
【解析】
求出函数的定义域,函数的导数,通过a的范围讨论,判断函数的单调性即可.(2)
对任意x>0,都有f(x)>0成立,转化为在(0,+∞)上f(x)min>0,利用函数的导数求解函数的最值即可.
(1)解:函数f(x)的定义域为(0,+∞)
又![]()
当a≤0时,在(0,+∞)上,f′(x)<0,f(x)是减函数
当a>0时,由f′(x)=0得:![]() 或
或![]() (舍)
(舍)
所以:在![]() 上,f′(x)<0,f(x)是减函数
上,f′(x)<0,f(x)是减函数
在![]() 上,f′(x)>0,f(x)是增函数
上,f′(x)>0,f(x)是增函数
(2)对任意x>0,都有f(x)>0成立,即:在(0,+∞)上f(x)min>0
由(1)知:当a≤0时,在(0,+∞)上f(x)是减函数,
又f(1)=2a﹣2<0,不合题意
当a>0时,当![]() 时,f(x)取得极小值也是最小值,
时,f(x)取得极小值也是最小值,
所以:![]()
令![]() (a>0)
(a>0)
所以:![]()
在(0,+∞)上,u′(a)>0,u(a)是增函数又u(1)=0
所以:要使得f(x)min≥0,即u(a)≥0,即a≥1,
故:a的取值范围为[1,+∞)


科目:高中数学 来源: 题型:
【题目】某学校为了解高三复习效果,从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩,分成6组制成频率分布直方图如图所示:
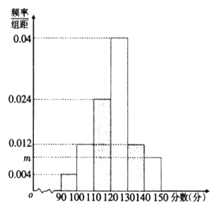
(1)求![]() 的值;并且计算这50名同学数学成绩的样本平均数
的值;并且计算这50名同学数学成绩的样本平均数![]() ;
;
(2)该学校为制定下阶段的复习计划,从成绩在![]() 的同学中选出3位作为代表进行座谈,记成绩在
的同学中选出3位作为代表进行座谈,记成绩在![]() 的同学人数位
的同学人数位![]() ,写出
,写出![]() 的分布列,并求出期望.
的分布列,并求出期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中a为常数).
(其中a为常数).
(1)当a=1时,求f(x)在![]() 上的值域;
上的值域;
(2)若当x∈[0,1]时,不等式![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)设![]() ,是否存在正数a,使得对于区间
,是否存在正数a,使得对于区间![]() 上的任意三个实数m,n,p,都存在以f(g(m)),f(g(n)),f(g(p))为边长的三角形?若存在,试求出这样的a的取值范围;若不存在,请说明理由.
上的任意三个实数m,n,p,都存在以f(g(m)),f(g(n)),f(g(p))为边长的三角形?若存在,试求出这样的a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国自改革开放以来,生活越来越好,肥胖问题也目渐显著,为分析肥胖程度对总胆固醇与空腹血糖的影响,在肥胖人群中随机抽出8人,他们的肥胖指数![]() 值、总胆固醇
值、总胆固醇![]() 指标值单位:
指标值单位: ![]() )、空腹血糖
)、空腹血糖![]() 指标值(单位:
指标值(单位: ![]() )如下表所示:
)如下表所示:

(1)用变量![]() 与
与![]() 与
与![]() 的相关系数,分别说明
的相关系数,分别说明![]() 指标值与
指标值与![]() 值、
值、![]() 指标值与
指标值与![]() 值的相关程度;
值的相关程度;
(2)求![]() 与
与![]() 的线性回归方程,已知
的线性回归方程,已知![]() 指标值超过5.2为总胆固醇偏高,据此模型分析当
指标值超过5.2为总胆固醇偏高,据此模型分析当![]() 值达到多大时,需要注意监控总胆固醇偏高情况的出现(上述数据均要精确到0.01)
值达到多大时,需要注意监控总胆固醇偏高情况的出现(上述数据均要精确到0.01)
参考公式:相关系数
 ,
,  ,
,![]() .
.
参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司每天从甲地运货物到乙地,统计最近的200次可配送的货物量,可得可配送的货物量的频率分布直方图,所图所示,回答以下问题(直方图中每个小组取中间值作为该组数据的替代值).
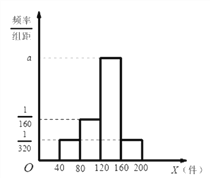
(1)求该物流公司每天从甲地到乙地平均可配送的货物量;
(2)该物流公司拟购置货车专门运营从甲地到乙地的货物,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40件货物,满载发车,否则不发车.若发车,则每辆车每趟可获利1000元;若未发车,则每辆车每天平均亏损200元.为使该物流公司此项业务的营业利润最大,该物流公司应该购置几辆货车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (k
(k![]() R),且满足f(﹣1)=f(1).
R),且满足f(﹣1)=f(1).
(1)求k的值;
(2)若函数y=f(x)的图象与直线![]() 没有交点,求a的取值范围;
没有交点,求a的取值范围;
(3)若函数![]() ,x
,x![]() [0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
[0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() (其中第一项是
(其中第一项是![]() ,接下来的
,接下来的![]() 项是
项是![]() ,再接下来的
,再接下来的![]() 项是
项是![]() ,依此类推)的前
,依此类推)的前![]() 项和为
项和为![]() ,下列判断:
,下列判断:
①![]() 是
是![]() 的第
的第![]() 项;②存在常数
项;②存在常数![]() ,使得
,使得![]() 恒成立;③
恒成立;③![]() ;④满足不等式
;④满足不等式![]() 的正整数
的正整数![]() 的最小值是
的最小值是![]() .
.
其中正确的序号是( )
A.①③B.①④C.①③④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com