
分析 ξ=6表示的试验结果是在1,2,3,4,5任取两球,再取6.
解答 解:一袋中装有大小相同的6个黑球,编号为1,2,3,4,5,6,
现从中随机取出3个球,以ξ表示取出的球的最大号码,
则ξ=6表示的试验结果是:
{1,2,6},{1,3,6},{1,4,6},{1,5,6},{2,3,6},{2,4,6},{2,5,6},{3,4,6},{3,5,6},{4,5,6}.
故答案为:{1,2,6},{1,3,6},{1,4,6},{1,5,6},{2,3,6},{2,4,6},{2,5,6},{3,4,6},{3,5,6},{4,5,6}.
点评 本题考查试验结果的表示,是基础题,解题时要认真审题,注意列举法的合理运用.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
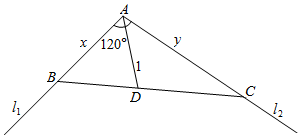 如图,某水域的两直线型岸边l1,l2 成定角120°,在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC(B,C分别在l1和l2上),围出三角形ABC养殖区,且AB和AC都不超过5公里.设AB=x公里,AC=y公里.
如图,某水域的两直线型岸边l1,l2 成定角120°,在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC(B,C分别在l1和l2上),围出三角形ABC养殖区,且AB和AC都不超过5公里.设AB=x公里,AC=y公里.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数|f(x)|为偶函数,且在(-∞,0)上单调递增 | |
| B. | 函数|f(x)|为奇函数,且在(-∞,0)上单调递增 | |
| C. | 函数f(|x|)为奇函数,且在(0,+∞)上单调递增 | |
| D. | 函数f(|x|)为偶函数,且在(0,+∞)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com