
分析 (1)将当a=0,b=1代入f(x)=-x2+ln(x+1),求导,当f′(x)>0,f(x)单调递增,f′(x)<0,f(x)单调递减,分别求得x的解集;
(2)根据切线方程求得a、b的值,f′(x)=ex-1-2x,判断f′(x)的单调性,求得出f(x)的最值f(x0),只需要证明f(x0)=${e}^{{x}_{0}-1}$-${x}_{0}^{2}$<$\frac{\sqrt{2}}{2}$,x0∈(0,$\frac{1}{2}$),f(${e}^{{x}_{0}-1}-{x}_{0}^{2}$<$\frac{1}{\sqrt{e}}$<$\frac{1}{\sqrt{2}}$$\frac{\sqrt{2}}{2}$.
解答 解:(1)当a=0,b=1时,已知函数f(x)=-x2+ln(x+1),
f′(x)=-2x+$\frac{1}{x+1}$=$\frac{-2{x}^{2}-2x+1}{x+1}$,
令f′(x)>0,解得:-1<x<$\frac{\sqrt{3}-1}{2}$,
f′(x)<0,解得:x>$\frac{\sqrt{3}-1}{2}$,
∴所以增区间是(-1,$\frac{\sqrt{3}-1}{2}$),减区间是($\frac{\sqrt{3}-1}{2}$,+∞);
(2)证明:由切线方程可知:切点(0,$\frac{1}{e}$),切线斜率为$\frac{1}{e}$,
∴f(0)=$\frac{a}{e}$=$\frac{1}{e}$,
∵f′(x)=aex-1-2x+$\frac{b}{x+1}$,
∴f′(x)=$\frac{a}{e}$+b=$\frac{1}{e}$,
∴a=1,b=0;
f′(x)=ex-1-2x,设g(x)=ex-1-2x,
在(-1,1)上g′(x)=ex-1-2<0,
∴g(x)是减函数,即f′(x)在(-1,1)是减函数,
f′(-1)=e-2+2>0,f′(-1)=-2<0,
f′(x)在(-1,1)内只有一个根x0,
在(-1,x0)f′(x)>0,f(x)增函数;在(x0,1)上f′(x)<0,f(x)减函数;
f(x0)是极大值,也是最大值,
只需要证明f(x0)=${e}^{{x}_{0}-1}$-${x}_{0}^{2}$<$\frac{\sqrt{2}}{2}$,
∵f′(0)=e-1>0,f′($\frac{1}{2}$)=${e}^{-\frac{1}{2}}$-1=$\frac{1}{\sqrt{e}}-1$<0,
∴x0∈(0,$\frac{1}{2}$),
${e}^{{x}_{0}-1}<{e}^{\frac{1}{2}-1}$=$\frac{1}{\sqrt{e}}$,-${x}_{0}^{2}$<0,
∴f(${e}^{{x}_{0}-1}-{x}_{0}^{2}$<$\frac{1}{\sqrt{e}}$<$\frac{1}{\sqrt{2}}$$\frac{\sqrt{2}}{2}$.
点评 本题考查根据导函数求函数的单调性,及求切线方程,过程繁琐,属于难题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | q>0时,数列{bn}中的项都是正数 | B. | 数列{an}中一定存在的为负数的项 | ||
| C. | 数列{an}中至少有三项是正数 | D. | 以上说法都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
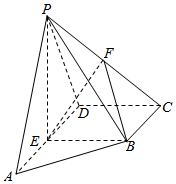 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,四边形ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=$\frac{1}{2}$AD=1,PA=PD,E,F分别为线段AD,PC的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,四边形ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=$\frac{1}{2}$AD=1,PA=PD,E,F分别为线段AD,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com