
分析 (Ⅰ)直接由等差数列的求和公式得到Sn.再把n=1,2,3,4,5分别代入即可求出集合A;
(Ⅱ)${S}_{n}=n{a}_{1}+\frac{n(n-1)d}{2}$=$\frac{2}{3}[n+\frac{n(n-1)}{2}]$=$\frac{n(n+1)}{3}$,Sn中的整数项按从小到大的顺序构成数列{cn},可得n=3k或n+1=3k(k∈Z);
(Ⅲ)由于{bn}的前n项和为Tn.故应分类讨论,然后利用Tk,T2k同时为集合A中的元素进行求解.
解答 解:(Ⅰ)∵等差数列{an}首项和公差都是$\frac{2}{3}$,
∴${S}_{n}=n{a}_{1}+\frac{n(n-1)d}{2}$=$\frac{2}{3}[n+\frac{n(n-1)}{2}]$=$\frac{n(n+1)}{3}$.
把n=1,2,3,4,5分别代入上式,得
A={$\frac{2}{3}$,2,4,$\frac{20}{3}$,10};
(Ⅱ)由(Ⅰ)得,${S}_{n}=\frac{n(n+1)}{3}$,
∵Sn中的整数项按从小到大的顺序构成数列{cn},∴n=3k或n+1=3k(k∈Z),
故可求cn=n(3n+1),或cn=n(3n-1);
(Ⅲ)当q=1时,Tk=kb1,T2k=2kb1;
∴T2k=2Tk;
∵Tk,T2k同时为集合A中的元素,
∴Tk=2,T2k=4,得kb1=2,
∴b1=$\frac{2}{k}$,
∴bn=$\frac{2}{k}$;
当q≠1时,Tk=$\frac{{b}_{1}(1-{q}^{k})}{1-q}$,T2k=$\frac{{b}_{1}(1-{q}^{2k})}{1-q}$,$\frac{{T}_{2k}}{{T}_{k}}=1+{q}^{k}$,
∵q为正整数,正整数k大于1.
∴当Tk=$\frac{2}{3}$时,T2k=$\frac{20}{3}$,得到qk=9,此时q=3,k=2,
∴Tk=T2=b1(1+q)=b1×4=$\frac{2}{3}$,得b1=$\frac{1}{6}$,故${b}_{n}=\frac{1}{6}$×3n-1=$\frac{1}{2}$×3n-2;
当Tk=2时,T2k=10,得到qk=4,此时q=2,k=2,
∴Tk=T2=b1(1+q)=b1×3=2,得b1=$\frac{2}{3}$,bn=$\frac{2}{3}$×2n-1=$\frac{1}{3}$×2n;
当Tk=4,${T}_{k}=\frac{20}{3}$,Tk=10时,找不到满足条件的{bn}.
点评 本题考查数列递推式,考查了数列的函数特性,考查等差数列、等比数列的求和公式,考查逻辑思维能力和转化能力,难度较大.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
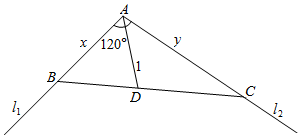 如图,某水域的两直线型岸边l1,l2 成定角120°,在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC(B,C分别在l1和l2上),围出三角形ABC养殖区,且AB和AC都不超过5公里.设AB=x公里,AC=y公里.
如图,某水域的两直线型岸边l1,l2 成定角120°,在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC(B,C分别在l1和l2上),围出三角形ABC养殖区,且AB和AC都不超过5公里.设AB=x公里,AC=y公里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com