
| A. | q>0时,数列{bn}中的项都是正数 | B. | 数列{an}中一定存在的为负数的项 | ||
| C. | 数列{an}中至少有三项是正数 | D. | 以上说法都不对 |
分析 不妨设等差数列{an}中的每一项如下:a1<a2<a3<…<an,其中an>0.如果数列{an}中至少有三项式正数,比如0<an-2<an-1<an,这时,an-2,an-1,an即是等差数列又是等比数列,可得:an-2=an-1=an,矛盾.即可得出.
解答 解:不妨设等差数列{an}中的每一项如下:a1<a2<a3<…<an,其中an>0.
如果数列{an}中至少有三项式正数,比如0<an-2<an-1<an,这时,an-2,an-1,an即是等差数列又是等比数列,即an-2=an-1=an,矛盾.
说明数列{an}中至多有两项是正数.
∴数列{an}中一定存在的为负数的项.
故选:B.
点评 本题考查了等差数列与等比数列的通项公式及其性质、反证法,考查了推理能力与计算能力,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
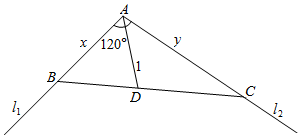 如图,某水域的两直线型岸边l1,l2 成定角120°,在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC(B,C分别在l1和l2上),围出三角形ABC养殖区,且AB和AC都不超过5公里.设AB=x公里,AC=y公里.
如图,某水域的两直线型岸边l1,l2 成定角120°,在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC(B,C分别在l1和l2上),围出三角形ABC养殖区,且AB和AC都不超过5公里.设AB=x公里,AC=y公里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com