
分析 (1)设{an}的奇数项构成的等差数列的公差为d,偶数项构成的等比数列的公比为q,运用通项公式,解方程可得d=2,q=3,即可得到所求通项公式;
(2)当k为奇数时,当k为偶数时,运用通项公式,解方程可得k的值;
(3)求得S2k,S2k-1,若$\frac{{{S_{2k}}}}{{{S_{2k-1}}}}$为数列{an}中的一项,整理化简求得k,m的值,再由数学归纳法证明,即可得到结论.
解答 解:(1)设{an}的奇数项构成的等差数列的公差为d,
偶数项构成的等比数列的公比为q,
则${a_{2n-1}}=1+(n-1)d,\;\;{a_{2n}}=2{q^{n-1}}$.
由已知,得$\left\{\begin{array}{l}2q=(2+d)+2\\ 1+4d=(1+d)+2q\end{array}\right.⇒\left\{\begin{array}{l}d=2\\ q=3.\end{array}\right.$
故数列{an}的通项公式为:${a_n}=\left\{\begin{array}{l}n,(当n为奇数)\\ 2•{3^{\frac{n-2}{2}}},(当n为偶数)\end{array}\right.$.
(2)当k为奇数时,由akak+1=ak+2,
得 $k•2•{3^{\frac{k-1}{2}}}=k+2\;⇒{3^{\frac{k-1}{2}}}=\frac{k+2}{2k}$.
由于${3^{\frac{k-1}{2}}}∈{N^*},而\frac{k+2}{2k}仅在k=2时为正整数,与k为奇数矛盾!$
当k为偶数时,由akak+1=ak+2,
得 $2•{3^{\frac{k-2}{2}}}•(k+1)=2•{3^{\frac{k}{2}}}\;⇒k=2$.
综上,得k=2.
(3)由(1)可求得${S_{2k}}=[{1+3+…+(2k-1)}]+2(1+3+{3^2}+…+{3^{k-1}})={3^k}+{k^2}-1$,${S_{2k-1}}={S_{2k}}-{a_{2k}}={3^{k-1}}+{k^2}-1$.
若$\frac{{{S_{2k}}}}{{{S_{2k-1}}}}$为数列{an}中的一项,
则$\frac{{{S_{2k}}}}{{{S_{2k-1}}}}=m(m为正奇数),或\frac{{{S_{2k}}}}{{{S_{2k-1}}}}=2•{3^{\frac{m-2}{2}}}(m为正偶数)$.
( i)若$\frac{{{S_{2k}}}}{{{S_{2k-1}}}}=m(m为正奇数)$,
则$\frac{{{3^k}+{k^2}-1}}{{{3^{k-1}}+{k^2}-1}}=m⇒(3-m){3^{k-1}}=(m-1)({k^2}-1)$.
当k=1时,m=3,结论成立;
当k≠1时,$\frac{{{3^{k-1}}}}{{{k^2}-1}}=\frac{m-1}{3-m}$,由$\frac{{{3^{k-1}}}}{{{k^2}-1}}>0,得\frac{m-1}{3-m}>0,解得1<m<3$,
由于m为正奇数,故此时满足条件的正整数k不存在.
( ii)若$\frac{{{S_{2k}}}}{{{S_{2k-1}}}}=2•{3^{\frac{m-2}{2}}}(m为正偶数)$,显然k≠1,
$\frac{{{3^k}+{k^2}-1}}{{{3^{k-1}}+{k^2}-1}}=2•{3^{\frac{m-2}{2}}}⇒(3-2•{3^{\frac{m-2}{2}}}){3^{k-1}}=({k^2}-1)(2•{3^{\frac{m-2}{2}}}-1)⇒\frac{{{3^{k-1}}}}{{{k^2}-1}}=\frac{{2•{3^{\frac{m-2}{2}}}-1}}{{3-2•{3^{\frac{m-2}{2}}}}}$.
由k>1得$\frac{{{3^{k-1}}}}{{{k^2}-1}}>0,得\frac{{2•{3^{\frac{m-2}{2}}}-1}}{{3-2•{3^{\frac{m-2}{2}}}}}>0⇒1<2•{3^{\frac{m-2}{2}}}<3$.$由m为正偶数,得2•{3^{\frac{m-2}{2}}}为正偶数$,
因此$2•{3^{\frac{m-2}{2}}}=2$,从而$\frac{{{3^{k-1}}}}{{{k^2}-1}}=1⇒{3^{k-1}}={k^2}-1$.
当k=2时,3k-1=k2-1;
下面用数学归纳法证明:当k≥3时,3k-1>k2-1.
①当k=3时,显然3k-1>k2-1;
②假设当k=l≥3时,有3l-1>l2-1;
当k=l+1时,由l≥3得3(l2-1)-[(l+1)2-1]=(l-1)2+(l2-4)>0,
故3(l+1)-1=3•3l-1>3(l2-1)>(l+1)2-1,
即当k=l+1时,结论成立.
由①,②知:当k≥3时,3k-1>k2-1.
综合( i),( ii)得:存在两个正整数k,k=1或2,使$\frac{{{S_{2k}}}}{{{S_{2k-1}}}}$为数列{an}中的项.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,注意运用分类讨论的思想方法和数学归纳法的证明,考查推理和运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
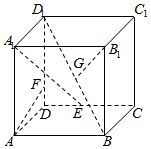 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | q>0时,数列{bn}中的项都是正数 | B. | 数列{an}中一定存在的为负数的项 | ||
| C. | 数列{an}中至少有三项是正数 | D. | 以上说法都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com