
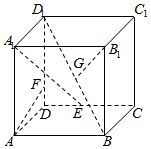
 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据直线与直线、直线与平面的位置关系,分别分析选项,利用排除法能得出结论
解答 解:因为DE⊥平面A1D,根据三垂线定理,
①对于任意给定的点E,A1E在平面A1D的射影为A1D,
所以存在点F,使得AF⊥A1D,所以AF⊥A1E;
②如果对于任意给定的点F,存在点E,使得AF⊥A1E;那么AF⊥A1D,又AD1⊥A1D,
得到过A有两条直线与A1D垂直,故②错误;
③只有AF垂直D1G在平面BCC1B1中的射影时,AF⊥B1G,
∴③正确;
④只有AF⊥平面A1CD1时,④才正确,
∵过A点作平面A1BD1的垂线与BB1无交点,
∴④错误.
故选:C.
点评 本题考查直线与直线、直线与平面的位置关系的判断,是中档题,解题时要注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{6}$ | B. | x=$\frac{5π}{12}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{7π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{2}$ | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com