
分析 (I)根据直线的参数方程得出直线l上的定点,和斜率,得出普通方程,将曲线C的极坐标方程两边同乘ρ展开得出曲线C的普通方程;
(II)求出l的垂线方程,解方程组得出H的参数方程.化成普通方程判断曲线类型.
解答 解:(I)直线l的普通方程为$\frac{x}{cosφ}$=$\frac{y+1}{sinφ}$,即y=tanφ•x-1.
∵ρ=2sin(θ+$\frac{π}{3}$),∴ρ2=ρsinθ+$\sqrt{3}$ρcosθ,
∴曲线C的普通方程为x2+y2-$\sqrt{3}$x-y=0.
(II)由直线l的参数方程可知直线l的斜率为tanφ,
∴过点B(0,1)且与直线l垂直的直线方程为y=-$\frac{1}{tanφ}$x+1.
联立方程组$\left\{\begin{array}{l}{y=tanφ•x-1}\\{y=-\frac{1}{tanφ}•x-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{2tanφ}{1+ta{n}^{2}φ}}\\{y=\frac{ta{n}^{2}φ-1}{1+ta{n}^{2}φ}}\end{array}\right.$.
∴动点H轨迹的参数方程是$\left\{\begin{array}{l}{x=\frac{2tanφ}{1+ta{n}^{2}φ}}\\{y=\frac{ta{n}^{2}φ-1}{1+ta{n}^{2}φ}}\end{array}\right.$(φ是参数).
化成普通方程得x2+y2=1.
∴H点的轨迹表示单位圆.
点评 本题考查了参数方程,极坐标方程与普通方程的转化,参数方程的求解,属于中档题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
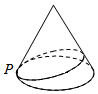 如图,一竖立在水平对面上的圆锥形物体的母线长为4m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为$4\sqrt{3}m$,则圆锥底面圆的半径等于( )
如图,一竖立在水平对面上的圆锥形物体的母线长为4m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为$4\sqrt{3}m$,则圆锥底面圆的半径等于( )| A. | 1m | B. | $\frac{3}{2}m$ | C. | $\frac{4}{3}m$ | D. | 2m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
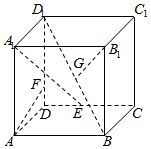 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com