
| A. | $±\sqrt{2}$ | B. | 0 | C. | 1 | D. | 2 |
分析 求定积分得到|z|,然后利用复数代数形式的乘除运算化简z,代入复数模的公式求得m的值.
解答 解:|z|=$\int_0^π{(sinx-\frac{1}{π}})dx$=(-cosx-$\frac{x}{π}$)${|}_{0}^{π}$=-cosπ-$\frac{π}{π}$-(-cos0-0)=1,
又z=$\frac{m}{1-i}$=$\frac{m(1+i)}{(1-i)(1+i)}=\frac{m}{2}(1+i)$,
∴$|\frac{m}{2}|•\sqrt{2}=1$,则m=$±\sqrt{2}$.
故选:A.
点评 本题考查定积分的求法,考查复数模的求法,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
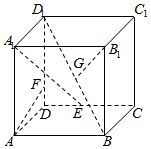 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,$\frac{{{e^2}-1}}{2e-1}$) | B. | (1,+∞) | C. | ($\frac{{{e^2}-1}}{2e-1}$,2) | D. | ($\frac{{{e^2}-1}}{2e-1}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com