
分析 直接利用基本不等式,即可求出logx9+log27x的最小值.
解答 解:∵x>1,
∴logx9>0,log27x>0,
∴${log_x}9+{log_{27}}x=\frac{2lg3}{lgx}+\frac{lgx}{3lg3}≥2\sqrt{\frac{2lg3}{lgx}•\frac{lgx}{3lg3}}=\frac{{2\sqrt{6}}}{3}$(当且仅当$\frac{2lg3}{lgx}=\frac{lgx}{3lg3}$,即$x={3^{\sqrt{6}}}$取等号).
故答案为:$\frac{{2\sqrt{6}}}{3}$.
点评 本题考查利用基本不等式求logx9+log27x的最小值,考查学生的计算能力,正确运用基本不等式是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
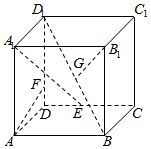 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,$\frac{{{e^2}-1}}{2e-1}$) | B. | (1,+∞) | C. | ($\frac{{{e^2}-1}}{2e-1}$,2) | D. | ($\frac{{{e^2}-1}}{2e-1}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com