
分析 (1)已知函数y=f(x)在$[-\frac{3π}{4},\frac{π}{3}]$上单调递增,且ω>0,利用正弦函数的单调性可得$\left\{{\begin{array}{l}{-\frac{3π}{4}ω≥-\frac{π}{2}}\\{\frac{π}{3}ω≤\frac{π}{2}}\end{array}}\right.$,即可得解ω的取值范围.
(2)利用变换法则“左加右减,上加下减”即可得到g(x)的解析式,令g(x)=0,即可解出零点的坐标,可得相邻两个零点之间的距离.若b-a最小,则a和b都是零点,此时在区间[a,mπ+a](m∈N*)恰有2m+1个零点,所以在区间[a,9π+a]是恰有19个零点,从而在区间(9π+a,b]至少有一个零点,即可得到a,b满足的条件.进一步即可得出b-a的最小值.
解答 解:(1)因为y=f(x)在$[-\frac{3π}{4},\frac{π}{3}]$上单调递增,ω>0,
根据题意有,$\left\{{\begin{array}{l}{-\frac{3π}{4}ω≥-\frac{π}{2}}\\{\frac{π}{3}ω≤\frac{π}{2}}\end{array}}\right.$,
所以:$0<ω≤\frac{2}{3}$.
(2)由题意:f(x)=2sin2x,
将函数y=f(x)的图象向左平移$\frac{π}{6}$个单位长度,再向上平移1个单位长度,得到函数解析式为:g(x)=2sin(2x+$\frac{π}{3}$)+1,
∵g(x)=0,可得:sin(2x+$\frac{π}{3}$)=-$\frac{1}{2}$,
∴x=kπ-$\frac{π}{4}$或x=kπ-$\frac{7π}{12}$,k∈Z,
即g(x)的零点相离间隔依次为$\frac{π}{3}$和$\frac{2π}{3}$,
∴若y=g(x)在[a,b]上至少含有20个零点,
∵若b-a最小,则a和b都是零点,此时在区间[a,π+a],[a,2π+a],…,[a,mπ+a](m∈N*)分别恰有3,5,…,2m+1个零点,
所以在区间[a,9π+a]是恰有19个零点,从而在区间(9π+a,b]至少有一个零点,
∴b-a-9π≥$\frac{π}{3}$,
则b-a的最小值为$\frac{28π}{3}$.
点评 本题综合考查了三角函数的单调性、周期性、函数的零点等基础知识与基本技能,考查了分析问题和解决问题的能力、推理能力和计算能力,属于中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | q>0时,数列{bn}中的项都是正数 | B. | 数列{an}中一定存在的为负数的项 | ||
| C. | 数列{an}中至少有三项是正数 | D. | 以上说法都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
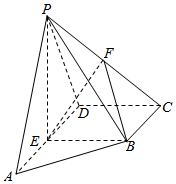 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,四边形ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=$\frac{1}{2}$AD=1,PA=PD,E,F分别为线段AD,PC的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,四边形ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=$\frac{1}{2}$AD=1,PA=PD,E,F分别为线段AD,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
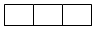 用2种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形中相邻矩形颜色不同的概率是( )
用2种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形中相邻矩形颜色不同的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com