
分析 (I)求函数的导数,利用导数的几何意义建立方程关系即可求实数a的值;
(Ⅱ)由题意分别求出函数的导数,再讨论①当c≤0时②当c>0时的情况,最后确定出c的取值范围.
解答 解:(I)f′(x)=$\frac{a}{x+1}$-2x-2,f(0)=-1,
则f′(0)=a-2,
∵f(x)在点(0,f(0))处的切线与x轴平行.
∴f′(0)=a-2=0,则a=2;
(Ⅱ)∵a=2,∴f(x)=2ln(x+1)-x2-2x-1,
g(x)=$\frac{1}{2}$[f(x)+(1+2c)x2+1]=$\frac{1}{2}$[2ln(x+1)-x2-2x-1+(1+2c)x2+1]=ln(x+1)+cx2-x,
由题意g′(x)=$\frac{1}{x+1}$+2cx-1=$\frac{x(2cx+2c-1)}{x+1}$
①当c≤0时,函数g(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
此时,不存在实数b∈(0,1),使得当x∈(-1,b]时,函数f(x)的最大值为g(b);
②当c>0时,令g′(x)=0有x=0或x=$\frac{1-2c}{2c}$=$\frac{1}{2c}$-1,
(a)当$\frac{1}{2c}$-1<0即c>$\frac{1}{2}$时,
函数g(x)在(-1,$\frac{1}{2c}$-1)和(0,+∞)上单调递增,
在($\frac{1}{2c}$-1,0)上单调递减,
要存在实数b∈(0,1),使得当x∈(-1,b]时,函数g(x)的最大值为g(b),
则g($\frac{1}{2c}$-1)<g(1),代入化简得ln2c+$\frac{1}{4c}$+ln2-1>0(1)
令h(c)=ln2c+$\frac{1}{4c}$+ln2-1,c>$\frac{1}{2}$,
∵h′(c)=$\frac{1}{c}$(1-$\frac{1}{4c}$)>0恒成立,
故恒有h(c)>h($\frac{1}{2}$)=ln2-$\frac{1}{2}$>0,
∴c>$\frac{1}{2}$时,(1)式恒成立;
(b)当$\frac{1}{2c}$-1>0,即0<c<$\frac{1}{2}$时,函数g(x)在(-1,0)和($\frac{1}{2c}$-1,+∞)上单调递增,
在(0,$\frac{1}{2c}$-1)上单调递减,
此时由题,只需g(1)>0,解得c>1-ln2,
又$1-ln2<\frac{1}{2}$,
∴此时实数c的取值范围是1-ln2<c<$\frac{1}{2}$;
(c)当c=$\frac{1}{2}$时,函数g(x)在(-1,+∞)上单调递增,显然符合题意;
综上,实数c的取值范围是(1-ln2,+∞).
点评 本题主要考查导数的综合应用,求函数的导数,利用导数的几何意义求出切线斜率以及构造函数,研究函数的单调性和最值是解决本题的关键.综合性较强,难度较大.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
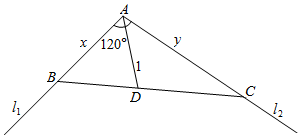 如图,某水域的两直线型岸边l1,l2 成定角120°,在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC(B,C分别在l1和l2上),围出三角形ABC养殖区,且AB和AC都不超过5公里.设AB=x公里,AC=y公里.
如图,某水域的两直线型岸边l1,l2 成定角120°,在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC(B,C分别在l1和l2上),围出三角形ABC养殖区,且AB和AC都不超过5公里.设AB=x公里,AC=y公里.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.984×0.02 | B. | 0.98×0.24 | C. | ${C}_{5}^{4}$×0.984×0.02 | D. | ${C}_{5}^{4}$×0.98×0.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com