
已知函数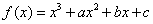 (实数
(实数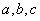 为常数)的图象过原点, 且在
为常数)的图象过原点, 且在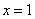 处的切线为直线
处的切线为直线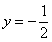 .(1)求函数
.(1)求函数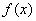 的解析式;(2)若常数
的解析式;(2)若常数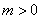 ,求函数
,求函数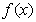 在区间
在区间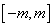 上的最大值.
上的最大值.
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
函数的极值
(1)判断函数极值的方法
①如果在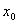 附近的左侧
附近的左侧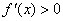 ,右侧
,右侧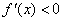 ,那么
,那么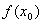 是_____.
是_____.
②如果在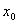 附近的左侧
附近的左侧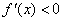 ,右侧
,右侧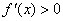 ,那么
,那么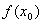 是______.
是______.
(2)若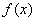 在
在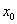 处取得极值,则_______
处取得极值,则_______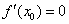 ;反之,若
;反之,若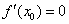 ,则
,则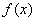 _______取得极值。例如:若
_______取得极值。例如:若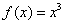 ,则
,则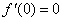 ,而
,而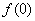 却不是
却不是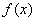 的极值(想一想?)
的极值(想一想?)
(3)求可导函数极值的步骤: ①求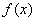 的定义域 ②求导数
的定义域 ②求导数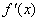 ③求导数
③求导数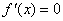 的根④列表,判断
的根④列表,判断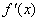 在方程的根的左右值的符号,确定
在方程的根的左右值的符号,确定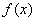 在这个根处是取极大值还是取极小值.
在这个根处是取极大值还是取极小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某工厂共有10台机器,生产一种仪器元件,由于受生产能力和技术水平等因素限制,会产生一定数量的次品.根据经验知道,每台机器产生的次品数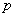 (万件)与每台机器的日产量
(万件)与每台机器的日产量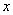 (万件)
(万件)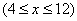 之间满足关系:
之间满足关系: 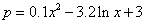 .已知每生产1万件合格的元件可以盈利2万元,但每产生1万件次品将亏损1万元.(利润=盈利—亏损)
.已知每生产1万件合格的元件可以盈利2万元,但每产生1万件次品将亏损1万元.(利润=盈利—亏损)
(1)试将该工厂每天生产这种元件所获得的利润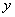 (万元)表示为
(万元)表示为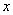 的函数;
的函数;
(2)当每台机器的日产量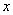 (万件)为多少时所获得的利润最大,最大利润为多少?
(万件)为多少时所获得的利润最大,最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com