
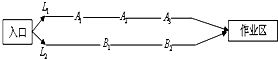
 某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有L1,L2两条巷道通往作业区(如图),L1巷道有A1,A2,A3三个易堵塞点,各点被堵塞的概率都是| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
| C | 0 3 |
| 1 |
| 2 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
| 1 |
| 10 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
| 9 |
| 20 |
| 3 |
| 4 |
| 3 |
| 5 |
| 9 |
| 20 |
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 1 |
| 10 |
| 9 |
| 20 |
| 9 |
| 20 |
| 27 |
| 20 |
| C | 0 3 |
| 1 |
| 2 |
| 1 |
| 8 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| C | 3 3 |
| 1 |
| 2 |
| 1 |
| 8 |
| Y | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 1 |
| 8 |
| 3 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.查看答案和解析>>
科目:高中数学 来源: 题型:
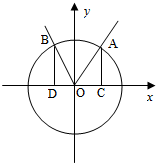 如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=
如图,在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在单位平面上,∠xOA=α,∠AOB=| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| ||
| 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| m-4 |
| y2 |
| 6-m |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com