
| A. | $\frac{32}{3}$(1-$\frac{1}{{4}^{n}}$) | B. | $\frac{32}{3}$(1-$\frac{1}{{2}^{n}}$) | C. | 16(1-$\frac{1}{{4}^{n}}$) | D. | 16(1-$\frac{1}{{2}^{n}}$) |
分析 推导出{anan+1}是以8为首项,$\frac{1}{4}$为公比的等比数列,由此能出a1a2+a2a3+…+anan+1.
解答 解:∵等比数列{an}中,a2=2,a5=$\frac{1}{4}$,
∴$\left\{\begin{array}{l}{{a}_{2}={a}_{1}q=2}\\{{a}_{5}={a}_{1}{q}^{4}=\frac{1}{4}}\end{array}\right.$,解得${a}_{1}=4,q=\frac{1}{2}$,
∴${a}_{n}{a}_{n+1}=(4×\frac{1}{{2}^{n-1}})(4×\frac{1}{{2}^{n}})$=8×$\frac{1}{{4}^{n-1}}$,
∴{anan+1}是以8为首项,$\frac{1}{4}$为公比的等比数列,
∴a1a2+a2a3+…+anan+1=$\frac{8(1-\frac{1}{{4}^{n}})}{1-\frac{1}{4}}$=$\frac{32}{3}$(1-$\frac{1}{{4}^{n}}$).
故选:A.
点评 本题考查数列有前n项和的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤1 | B. | a≥1 | C. | a≤2 | D. | a≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
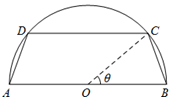 一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,直四棱柱木梁的体积为V(单位:m3),侧面积为S(单位:m2).
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,直四棱柱木梁的体积为V(单位:m3),侧面积为S(单位:m2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com