
分析 f(0)=20=1,故①正确;f(1)=2,故②错误;根据分数指数幂的运算性质可知③正确,④错误;根据基本不等式和分数指数幂的运算性质可知⑤正确,⑥错误.
解答 解:对于①:f(0)=20=1,故①正确;
对于②:f(1)=2,故②错误;
对于③:根据分数指数幂的运算性质可知,f(x1+x2)=2x1+x2=${2}^{{x}_{1}}•{2}^{{x}_{2}}$=f(x1)•f(x2),故③正确;
对于④:根据分数指数幂的运算性质可知,f(x1•x2)=${2}^{{x}_{1}•{x}_{2}}$=${(2}^{{x}_{1}})^{{x}_{2}}$,$f({x}_{1})+f({x}_{2})={2}^{{x}_{1}}+{2}^{{x}_{2}}$.则f(x1•x2)≠f(x1)+f(x2),故④错误;
对于⑤⑥:根据基本不等式和分数指数幂的运算性质可知.由于$\frac{f({x}_{1})+f({x}_{2})}{2}$=$\frac{{2}^{{x}_{1}}+{2}^{{x}_{2}}}{2}$$>\frac{2\sqrt{{2}^{{x}_{1}}•{2}^{{x}_{2}}}}{2}=\sqrt{{2}^{{x}_{1}}•{2}^{{x}_{2}}}$,$f(\frac{{x}_{1}+{x}_{2}}{2})={2}^{\frac{{x}_{1}+{x}_{2}}{2}}$=${(2}^{{x}_{1}+{x}_{2}})^{\frac{1}{2}}=\sqrt{{2}^{{x}_{1}}•{2}^{{x}_{2}}}$,
所以$f(\frac{{x}_{1}+{x}_{2}}{2})<\frac{f({x}_{1})+f({x}_{2})}{2}$,故⑤正确,⑥错误.
故答案为:①③⑤.
点评 本题主要考查了分数指数幂的基本运算性质,以及基本不等式的应用,属于知识的简单综合应用.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
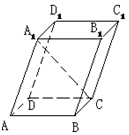 如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为1的正方形,若∠A1AB=∠A1AD=60°,且A1C=$\sqrt{5}$,则A1A=3.
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为1的正方形,若∠A1AB=∠A1AD=60°,且A1C=$\sqrt{5}$,则A1A=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{20}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com