
| 2 |
| an |
| 2 |
| an-1 |
| 1 |
| 1+an |
| 2 |
| an |
| 2 |
| an-1 |
| 1 |
| 1+an |
| 1 |
| bn |
| 1 |
| 1+an |
| 3 |
| 22k-1+1 |
| 3 |
| 22k-1 |
| 2 |
| an |
| 2 |
| an-1 |
| 2 |
| a1 |
| 2 |
| an |
| 1 |
| 1+an |
| 1 |
| bn |
| 1 |
| bn+1 |
| 2 | ||
|
| 1-bn+1 |
| bn+1 |
| 2bn |
| 1-bn |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 1+an |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 | ||
1-(-
|
| 3 | ||
1-(-
|
| 3 |
| |(-2)n-1| |
| 3 |
| 22k-1+1 |
| 3 |
| 22k-1 |
| 1 |
| 22k-1+1 |
| 1 |
| 22k-1 |
| 22k-1+22k |
| 24k-1+22k-1-1 |
| 22k-1+22k |
| 24k-1 |
| 1 |
| 22k-1 |
| 1 |
| 22k |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 22k |
| 1 |
| 22k |
| 1 |
| 22k |
| 3 |
| 22k+1+1 |
| 1 |
| 22k+1+1 |
| 1 |
| 22k |


科目:高中数学 来源: 题型:
 某学校进行自主实验教育改革,选取甲、乙两个班做对比实验,甲班采用传统教育方式,乙班采用学生自主学习,学生可以针对自己薄弱学科进行练习,教师不做过多干预,两班人数相同,为了检验教学效果,现从两班各随机抽取20名学生的期末总成绩,得到以下的茎叶图:
某学校进行自主实验教育改革,选取甲、乙两个班做对比实验,甲班采用传统教育方式,乙班采用学生自主学习,学生可以针对自己薄弱学科进行练习,教师不做过多干预,两班人数相同,为了检验教学效果,现从两班各随机抽取20名学生的期末总成绩,得到以下的茎叶图:| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
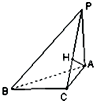 如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值.
如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值.查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 12 |
| π |
| 2 |
| 7π |
| 4 |
| π |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com