解:(Ⅰ)求导函数,可得f'(x)=3x
2+2ax+b
∵函数f(x)=x
3+ax
2+bx+c(x∈R)在
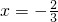
处取得极值,其图象在点(1,f(1))处的切线与直线y+2=0平行
∴
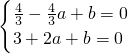
,∴a=-

,b=-2
(Ⅱ)对x∈[-1,2]都有f(x)<c
2恒成立,等价于对x∈[-1,2]都有x
3-

x
2-2x<c
2-c恒成立,
设y=x
3-

x
2-2x,则y′=3x
2-x-2=(x-1)(3x+2)
解(x-1)(3x+2)=0得x=-

或x=1
当x∈(-1,-

)时,y'>0;当x∈(-

,1)时,y'<0;当x∈(1,2)时,y'>0
则f(x)极大值=
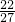
,f(x)极小值=-

又f(-1)=

,f(2)=2,所以f(x)
最大值=2;
∴2<c
2-c
∴c<-1或c>2.
分析:(Ⅰ)求导函数,根据函数f(x)=x
3+ax
2+bx+c(x∈R)在
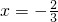
处取得极值,其图象在点(1,f(1))处的切线与直线y+2=0平行,建立方程,即可求a,b的值;
(Ⅱ)依题意得对x∈[-1,2]都有x
3-

x
2-2x<c
2-c恒成立,利用导数法,确定左边对应函数的最大值,可得不等式,从而可求c的取值范围.
点评:本题考查导数知识的运用,考查函数的极值与最值,考查导数的几何意义,考查恒成立问题,确定函数的单调性,求最值是关键.

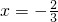 处取得极值,其图象在点(1,f(1))处的切线与直线y+2=0平行.
处取得极值,其图象在点(1,f(1))处的切线与直线y+2=0平行.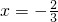 处取得极值,其图象在点(1,f(1))处的切线与直线y+2=0平行
处取得极值,其图象在点(1,f(1))处的切线与直线y+2=0平行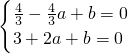 ,∴a=-
,∴a=- ,b=-2
,b=-2 x2-2x<c2-c恒成立,
x2-2x<c2-c恒成立, x2-2x,则y′=3x2-x-2=(x-1)(3x+2)
x2-2x,则y′=3x2-x-2=(x-1)(3x+2) 或x=1
或x=1 )时,y'>0;当x∈(-
)时,y'>0;当x∈(- ,1)时,y'<0;当x∈(1,2)时,y'>0
,1)时,y'<0;当x∈(1,2)时,y'>0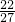 ,f(x)极小值=-
,f(x)极小值=-
 ,f(2)=2,所以f(x)最大值=2;
,f(2)=2,所以f(x)最大值=2;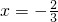 处取得极值,其图象在点(1,f(1))处的切线与直线y+2=0平行,建立方程,即可求a,b的值;
处取得极值,其图象在点(1,f(1))处的切线与直线y+2=0平行,建立方程,即可求a,b的值; x2-2x<c2-c恒成立,利用导数法,确定左边对应函数的最大值,可得不等式,从而可求c的取值范围.
x2-2x<c2-c恒成立,利用导数法,确定左边对应函数的最大值,可得不等式,从而可求c的取值范围.

 金钥匙试卷系列答案
金钥匙试卷系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<