
分析 (1)由Sn与an的关系,我们从n=1依次代入整数值,即可求出a1,a2,a3;
(2)由a1,a2,a3的值与n的关系,我们归纳推理出数列的通项公式,观察到它们是与自然数集相关的性质,故可采用数学归纳法来证明.
解答 解 (1)a1=1,a2=$\sqrt{2}$-1,a3=$\sqrt{3}$-$\sqrt{2}$.
(2)猜想an=$\sqrt{n}$-$\sqrt{n-1}$.
证明:①当n=1时,由a1=$\sqrt{1}$=1得结论成立;
②假设n=k(k∈N*)时结论成立,
即ak=$\sqrt{k}$-$\sqrt{k-1}$.
当n=k+1时,
ak+1=Sk+1-Sk=$\frac{1}{2}$(ak+1+$\frac{1}{ak+1}$)-$\frac{1}{2}$(ak+$\frac{1}{ak}$)
=$\frac{1}{2}$(ak+1+$\frac{1}{ak+1}$)-$\frac{1}{2}$($\sqrt{k}$-$\sqrt{k-1}$+$\frac{1}{\sqrt{k}-\sqrt{k-1}}$),
从而有ak+12+2$\sqrt{k}$ak+1-1=0,
又由ak+1>0,
解得ak+1=$\frac{-2\sqrt{k}+\sqrt{4k+4}}{2}$=$\sqrt{k+1}$-$\sqrt{k}$,
这说明当n=k+1时结论成立.
由①②可知,an=$\sqrt{n}$-$\sqrt{n-1}$对任意正整数n都成立.
点评 本题(2)中的证明要用到数学归纳法,数学归纳法常常用来证明一个与自然数集N相关的性质,其步骤为:设P(n)是关于自然数n的命题,若1)(奠基) P(n)在n=1时成立;2)(归纳) 在P(k)(k为任意自然数)成立的假设下可以推出P(k+1)成立,则P(n)对一切自然数n都成立


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)=ax+1(a>0,a≠1)的图象过定点(-1,1) | |
| B. | 函数$f(x)={x^{\frac{1}{2}}}$在[0,+∞)上是增函数 | |
| C. | 函数f(x)=logax(a>0,a≠1)在(0,+∞)上是增函数 | |
| D. | 函数f(x)=x2+4x+2在(0,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
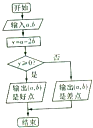 执行如图程序框图后,记“输出(a,b)是好点”为事件A.
执行如图程序框图后,记“输出(a,b)是好点”为事件A.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\sqrt{6}]$ | B. | (-∞,2] | C. | $[{\sqrt{6},+∞})$ | D. | [0,$\sqrt{6}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com