
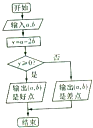
 执行如图程序框图后,记“输出(a,b)是好点”为事件A.
执行如图程序框图后,记“输出(a,b)是好点”为事件A.分析 (1)由题意,若a为区间[0,5]内的整数值随机数,b为区间[0,2]内的整数值随机数,则可产生6×3=18个点,事件A发生,则a≥2b,求出事件数,然后直接利用古典概型概率计算公式求解;
(2)由题意求出点(a,b)所构成的矩形面积,再由线性规划知识求出满足a≥2b的区域面积,由测度比是面积比求概率.
解答  解:(1)由题意,若a为区间[0,5]内的整数值随机数,b为区间[0,2]内的整数值随机数,则可产生6×3=18个点,事件A发生,则a≥2b,好点为(0,0),(1,0),(2,0),(2,1),(3,0),(3,1),(4,0),(4,1),(4,2),(5,0),(5,1),(5,2),共12个点,
解:(1)由题意,若a为区间[0,5]内的整数值随机数,b为区间[0,2]内的整数值随机数,则可产生6×3=18个点,事件A发生,则a≥2b,好点为(0,0),(1,0),(2,0),(2,1),(3,0),(3,1),(4,0),(4,1),(4,2),(5,0),(5,1),(5,2),共12个点,
∴P(A)=$\frac{12}{18}$=$\frac{2}{3}$;
(2)由题意,试验的全部结果构成的区域D={(a,b)|0≤a≤5,0≤b≤2},其面积为10;构成事件A的区域A={(a,b)|0≤a≤5,0≤b≤2,a≥2b},其面积为$\frac{1+5}{2}×2$=6,
∴P(A)=$\frac{6}{10}$=$\frac{3}{5}$.
点评 1本题考查了古典概型及其概率计算公式,考查了几何概型的概率,关键是理解(2)的测度比,是基础题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,N为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,N为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=2x | B. | y2=4x | C. | y2=6x | D. | y2=8x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或-2 | B. | $-\frac{2}{3}$ | C. | 1 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com