
分析 (1)由数列{an}的递推公式依次求出a2,a3,a4;
(2)根据a2,a3,a4值的结构特点猜想{an}的通项公式,再用数学归纳法①验证n=1成立,②假设n=k时命题成立,证明当n=k+1时命题也成立
解答 解:(1)令n=1,-2a2+3=0,a2=$\frac{3}{2}$,
令n=2,-$\frac{3}{2}$a3-$\frac{3}{2}$+4=0,a3=$\frac{5}{3}$,
令n=3,-$\frac{4}{3}$a4-$\frac{5}{3}$+4=0,a4=$\frac{7}{4}$.
(2)猜想an=$\frac{2n-1}{n}$(n∈N*).
证明:当n=1时,a1=1=$\frac{2-1}{1}$,所以an=$\frac{2n-1}{n}$成立,
假设当n=k时,an=$\frac{2n-1}{n}$成立,即ak=$\frac{2k-1}{k}$,
则(ak-3)ak+1-ak+4=0,即($\frac{2k-1}{k}$-3)ak+1-$\frac{2k-1}{k}$+4=0,
所以$\frac{k+1}{k}$ak+1=$\frac{2k+1}{k}$,即ak+1=$\frac{2k+1}{k+1}$=$\frac{2(k+1)-1}{k+1}$,
所以当n=k+1时,结论an=$\frac{2n-1}{n}$成立.
综上,对任意的n∈N*,an=$\frac{2n-1}{n}$成立.
点评 本题考查数列递推关系式的应用,数学归纳法证明数列问题的方法,考查逻辑推理能力,计算能力.注意在证明n=k+1时用上假设,化为n=k的形式,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -3 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)=ax+1(a>0,a≠1)的图象过定点(-1,1) | |
| B. | 函数$f(x)={x^{\frac{1}{2}}}$在[0,+∞)上是增函数 | |
| C. | 函数f(x)=logax(a>0,a≠1)在(0,+∞)上是增函数 | |
| D. | 函数f(x)=x2+4x+2在(0,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<f(-2)<f(3) | B. | f(-2)<f(1)<f(3) | C. | f(3)<f(-2)<f(1) | D. | f(3)<f(1)<f(-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
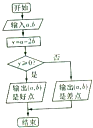 执行如图程序框图后,记“输出(a,b)是好点”为事件A.
执行如图程序框图后,记“输出(a,b)是好点”为事件A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com