
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若函数![]() 在
在![]() 处取得极大值,求实数
处取得极大值,求实数![]() 的取值范围
的取值范围
科目:高中数学 来源: 题型:
【题目】盒子里放有外形相同且编号为1,2,3,4,5的五个小球,其中1号与2号是黑球,3号、4号与5号是红球,从中有放回地每次取出1个球,共取两次.
(1)求取到的2个球中恰好有1个是黑球的概率;
(2)求取到的2个球中至少有1个是红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
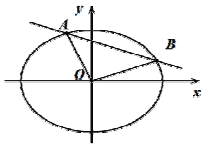
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() ,设线段
,设线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 的面积为
的面积为![]() (其中
(其中![]() 为坐标原点)且
为坐标原点)且![]() 时,试问:在坐标平面上是否存在两个定点
时,试问:在坐标平面上是否存在两个定点![]() ,使得当直线
,使得当直线![]() 运动时,
运动时,![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象为不间断的曲线,定义域为
的图象为不间断的曲线,定义域为![]() ,规定:
,规定:
①如果对于任意![]() ,
,![]() 都有
都有![]() ,则称函数
,则称函数![]() 是凹函数.
是凹函数.
②如果对于任意![]() ,
,![]() 都有
都有![]() ,则称函数
,则称函数![]() 是凸函数.
是凸函数.
(1)若函数![]() (
(![]() 且
且![]() )是凹函数,试写出实数
)是凹函数,试写出实数![]() 的取值范围;(直接写出结果,无需证明);
的取值范围;(直接写出结果,无需证明);
(2)判断函数![]() 是凹函数还是凸函数,并加以证明;
是凹函数还是凸函数,并加以证明;
(3)若对任意的![]() 且
且![]() ,
,![]() ,试证明存在
,试证明存在![]() ,使
,使![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() 为实数).
为实数).
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)求![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(3)若存在两个不等实数![]() ,使方程
,使方程![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+2),g(x)=loga(2﹣x)(a>0,a≠1).
(1)求函数f(x)﹣g(x)的定义域;
(2)判断f(x)﹣g(x)的奇偶性并证明;
(3)求f(x)﹣g(x)>0中x取值范围,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】常州地铁项目正在紧张建设中,通车后将给市民出行带来便利.已知某条线路通车后,地铁的发车时间间隔 ![]() (单位:分钟)满足
(单位:分钟)满足![]() ,
,![]() .经测算,地铁载客量与发车时间间隔
.经测算,地铁载客量与发车时间间隔![]() 相关,当
相关,当![]() 时地铁为满载状态,载客量为1200人,当
时地铁为满载状态,载客量为1200人,当![]() 时,载客量会减少,减少的人数与
时,载客量会减少,减少的人数与![]() 的平方成正比,且发车时间间隔为2分钟时的载客量为560人,记地铁载客量为
的平方成正比,且发车时间间隔为2分钟时的载客量为560人,记地铁载客量为![]() .
.
⑴ 求![]() 的表达式,并求当发车时间间隔为6分钟时,地铁的载客量;
的表达式,并求当发车时间间隔为6分钟时,地铁的载客量;
⑵ 若该线路每分钟的净收益为![]() (元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?
(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com