
分析 (1)求出f′(x)=4ax3+2bx,利用导数的几何意义列出方程组,求出a,b,c,由此能求出y=f(x)的解析式.
(2)求出f′(x)=10x3-9x,利用导数性质能求出y=f(x)的单调递区间.
解答 解:(1)∵f(x)=ax4+bx2+c的图象经过点(0,1),
且在x=1处的切线方程是y=x-2,
∴f′(x)=4ax3+2bx,
∴$\left\{\begin{array}{l}{f(0)=c=1}\\{{f}^{'}(1)=4a+2b=1}\\{f(1)=a+b+c=-1}\end{array}\right.$,
解得a=$\frac{5}{2}$,b=-$\frac{9}{2}$,c=1,
∴y=f(x)的解析式为f(x)=$\frac{5}{2}{x}^{4}$-$\frac{9}{2}{x}^{2}$+1.
(2)f′(x)=10x3-9x,
由f′(x)=10x3-9x>0,得-$\frac{3\sqrt{10}}{10}$<x<0或x>$\frac{3\sqrt{10}}{10}$,
由f′(x)=10x3-9x<0,得x<-$\frac{3\sqrt{10}}{10}$或0<x<$\frac{3\sqrt{10}}{10}$,
∴y=f(x)的单调递增区间为(-$\frac{3\sqrt{10}}{10}$,0),($\frac{3\sqrt{10}}{10}$,+∞),
单调减区间为(-∞,-$\frac{3\sqrt{10}}{10}$),(0,$\frac{3\sqrt{10}}{3}$).
点评 本题考查函数的解析式的求法,考查函数的单调区间的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | y=x2-x+6 | B. | y=x2+x+6 | C. | y=x2-3x+6 | D. | y=x2+3x+6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,+∞] | B. | (-∞,2) | C. | [2,+∞) | D. | (log37,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
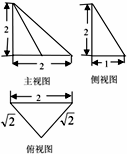
| A. | 1+$\sqrt{2}$+$\sqrt{3}$ | B. | 2+$\sqrt{2}$+$\sqrt{3}$ | C. | 3+$\sqrt{2}$+$\sqrt{3}$ | D. | 4+$\sqrt{2}$+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{\sqrt{x}}$ | B. | y=$\frac{lnx}{x}$ | C. | y=xex | D. | y=$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
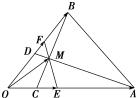 在△OAB中,$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{2}{5}$$\overrightarrow{OB}$,AD与BC交于点M,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.在线段AC上取一点E,在线段BD上取一点F,使EF过点M,设$\overrightarrow{OE}$=p$\overrightarrow{OA}$,$\overrightarrow{OF}$=q$\overrightarrow{OB}$.
在△OAB中,$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{2}{5}$$\overrightarrow{OB}$,AD与BC交于点M,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.在线段AC上取一点E,在线段BD上取一点F,使EF过点M,设$\overrightarrow{OE}$=p$\overrightarrow{OA}$,$\overrightarrow{OF}$=q$\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | 60 | C. | 120 | D. | 135 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com