
分析 由已知可得第四条直线与x-2y-1=0平行,且到x-2y-1=0的距离为$\frac{2}{\sqrt{5}}$,结合两线之间距离公式,可得答案.
解答 解:∵2x+y-1=0与2x+y+1=0的距离为$\frac{2}{\sqrt{5}}$,
故第四条直线与x-2y-1=0平行,且到x-2y-1=0的距离也为$\frac{2}{\sqrt{5}}$,
设第四条直线方程为x-2y+C=0,则$\frac{|C+1|}{\sqrt{5}}=\frac{2}{\sqrt{5}}$,
解得:C=1,或C=-3,
故第四条直线方程为x-2y+1=0或x-2y-3=0,
故答案为:x-2y+1=0或x-2y-3=0
点评 本题考查的知识点是待定系数法求直线的方程,其中正确理解第四条边直线的几何特征是解答的关键.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | π | C. | π2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 7 | 8 | 9 | 10 |
| P | 0.1 | 0.4 | 0.3 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
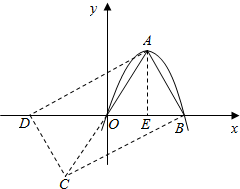 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 30° | C. | 150° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com