
【题目】已知函数![]() .
.
(1)设![]() ,求
,求![]() 的最大值及相应的
的最大值及相应的![]() 值;
值;
(2)对任意正数![]() 恒有
恒有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() 取得最大值
取得最大值![]() ;(2)
;(2)![]()
【解析】
(1)先化简函数g(x)=lnx﹣f′(x)f(x)=lnx﹣(2x﹣1)(x2﹣x),从而求定义域;再求导g′(x)![]() ;从而确定函数的最大值及相应的
;从而确定函数的最大值及相应的![]() 值;
值;
(2)f(x)+f(![]() )≥(x
)≥(x![]() )lnm可化为x2﹣x
)lnm可化为x2﹣x![]() (x
(x![]() )lnm;从而化为lnm
)lnm;从而化为lnm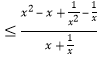 ;化简得
;化简得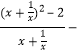 1=(x
1=(x![]() )
)![]() 1;从而利用换元法求函数的最值,从而化恒成立问题为最值问题.
1;从而利用换元法求函数的最值,从而化恒成立问题为最值问题.
(1)∵![]() ,∴
,∴![]() ,
,
∴![]()
![]()
则![]()
∵![]() 的定义域为
的定义域为![]() ,∴
,∴![]()
①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]()
因此![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
故当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
(2)由(1)可知,![]()
不等式![]() 可化为
可化为![]() ①
①
因为![]() ,所以
,所以![]() (当且仅当
(当且仅当![]() 取等号)
取等号)
设![]() ,则把①式可化为
,则把①式可化为![]() ,即
,即![]() (对
(对![]() 恒成立)
恒成立)
令![]() ,此函数在
,此函数在![]() 上是增函数,
上是增函数,
所以![]() 的最小值为
的最小值为![]()
于是![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
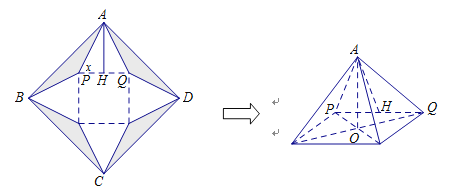
【题目】如图:设一正方形纸片ABCD边长为2分米,切去阴影部分所示的四个全等的等腰三角形,剩余为一个正方形和四个全等的等腰三角形,沿虚线折起,恰好能做成一个正四棱锥(粘接损耗不计),图中![]() ,O为正四棱锥底面中心.
,O为正四棱锥底面中心.
(Ⅰ)若正四棱锥的棱长都相等,求这个正四棱锥的体积V;
(Ⅱ)设等腰三角形APQ的底角为x,试把正四棱锥的侧面积S表示为x的函数,并求S的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学文化的优秀遗产,数学家刘徽在注解《九章算术》时,发现当圆内接正多边行的边数无限增加时,多边形的面积可无限逼近圆的面积,为此他创立了割圆术,利用割圆术,刘徽得到了圆周率精确到小数点后四位3.1416,后人称3.14为徽率,如图是利用刘徽的割圆术设计的程序框图,若结束程序时,则输出的![]() 为( )(
为( )(![]() ,
,![]() ,
,![]() )
)

A. 6 B. 12 C. 24 D. 48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]() 与拋物线C:
与拋物线C:![]() 相切.
相切.
(1)求拋物线方程;
(2)斜率不为0的直线![]() 经过拋物线C的焦点F,交抛物线于两点A,B,拋物线C上是否存在两点D,E关于直线
经过拋物线C的焦点F,交抛物线于两点A,B,拋物线C上是否存在两点D,E关于直线![]() 对称.若存在求出斜率k的取值范围;若不存在,说明理由.
对称.若存在求出斜率k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)由0,1,2,…,9这十个数字组成的无重复数字的四位数中,十位数字与千位数字之差的绝对值等于7的四位数的个数共有几种?
(2)我校高三学习雷锋志愿小组共有16人,其中一班、二班、三班、四班各4人,现在从中任选3人,要求这三人不能是同一个班级的学生,且在三班至多选1人,求不同的选取法的种数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:![]() ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.
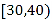
(1)现从年龄在![]() 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用![]() 表示年龄在
表示年龄在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() .当
.当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从学生文艺部6名成员(4男2女)中,挑选2人参加学校举办的文艺汇演活动.
(1)求男生甲被选中的概率;
(2)在已知男生甲被选中的条件下,女生乙被选中的概率;
(3)在要求被选中的两人中必须一男一女的条件下,求女生乙被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com