
(本小题满分10分)
如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G。
(1)求证:圆心O在直线AD上;
(2)求证:点C是线段GD的中点。
(1)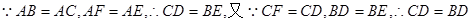
又△ABC是等腰三角形,所以AD是∠CAB的角分线
∴圆心O在直线AD上。(2))连接DF,由(I)知,DH是⊙O的直径, ∴∠DFH=90°,∴∠FDH+∠FHD=90°,又∠G+∠FHD=90°,∴∠FDH=∠G,又⊙O与AC相切于点F ,∴∠AFH=∠GCF=∠FHD ∴∠GCF=∠G,∴CG=CF=CD,∴点C是线段GD的中点。
解析试题分析:(I)证明:
又△ABC是等腰三角形,所以AD是∠CAB的角分线
∴圆心O在直线AD上。……………5分
(II)连接DF,由(I)知,DH是⊙O的直径,
∴∠DFH=90°,∴∠FDH+∠FHD=90°
又∠G+∠FHD=90°,∴∠FDH=∠G
又⊙O与AC相切于点F
∴∠AFH=∠GCF=∠FHD ∴∠GCF=∠G
∴CG=CF=CD
∴点C是线段GD的中点。 ………………10分
考点:圆的切线的性质定理证明。
点评:本题利用了切线的性质,四边形的内角和为360度及圆周角定理求解.属于基础题型。


科目:高中数学 来源: 题型:解答题
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,
且BC AE=DC
AE=DC AF,B、E、F、C四点共圆.
AF,B、E、F、C四点共圆.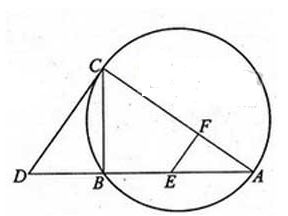
(Ⅰ)证明:CA是△ABC外接圆的直径;
(Ⅱ)若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知点M在菱形ABCD的BC边上,连结AM交BD于点E,过菱形ABCD的顶点C作CN∥AM,分别交BD、AD于点F、N,连结AF、CE.判断四边形AECF的形状,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于HH,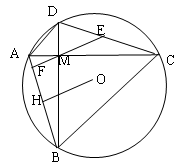
求证:(1)EF⊥AB (2)OH=ME
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)选修4—1:几何证明选讲
如图,四边形 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心,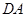 为半径的圆弧与以
为半径的圆弧与以 为直径的半圆
为直径的半圆 交于点
交于点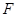 ,延长
,延长 交
交 于
于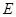 .
.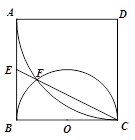
(1)求证: 是
是 的中点;
的中点;
(2)求线段 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com