
分析 (1)由f(-4n)=0,f'(0)=2n组成方程组,即可解得a,b,求出f(x)的解析式;
(2)f'(-n)=n,则an=n•2n,利用错位相减法即可求出前n项和.
解答 解:(1)∵f(x)的图象过点(-4n,0),
∴16n2a-4nb-0,…①
∵f'(x)=2ax+b,
∴f'(0)=b=2n,…②
由①②组成方程组解得:a=$\frac{1}{2}$,b=2n,
故f(x)=$\frac{1}{2}{x}^{2}+2nx$ (n∈N*);
(2)∵f'(x)=x+2n
∴f'(-n)=n,
∴an=n•2n,
记{an}的前n项和为Sn,
则Sn=2+2×22+3×23+…+n•2n,
∴2Sn=22+2×23+3×24+…+(n-1)•2n+n•2n+1,
∴-Sn=2+22+23+…+2n-n•2n+1=$\frac{2(1-{2}^{n})}{1-2}-n•{2}^{n+1}$=(1-n)•2n+1-2,
∴${S}_{n}=(n-1)•{2}^{n+1}+2$
点评 本题考察了导数的基本概念和利用错位相减法求数列的前n项和,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
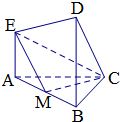 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-2016) | B. | (1,2016) | C. | (-1,2016) | D. | (1,-2016) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 真;¬p:?x<0,-x2+x-4>0 | B. | 真;¬p:?x<0,-x2+x-4≥0 | ||
| C. | 假;¬p:?x<0,-x2+x-4>0 | D. | 假;¬p:?x<0,-x2+x-4≥0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com